UPDATE 19/08/02: further analysis shows that the proposed experiment may be harder to do than I thought. The 1.1 nanometer electron wavelength is for a static electron–unlike photons, fermions have a wavelength that varies as their kinetic energy. To do the experiment, the electrons and positrons have to have some velocity, so the reduced wavelength and thus the experiment’s sensitivity to the different interference patterns may be out of reach of today’s technology. If we could propel the electron at very low speeds and still discern a quantum interference pattern, the experiment should still give us a distinguishable decision on the electron’s internal structure. It’s a little like using measurable quantum interference waves as a tomography scan to observe internal details too small to directly project to a detector. Unfortunately, now secondary effects such as the atomic effects of the barrier slit will start to predominate and the experiment will become more difficult to do and perhaps less conclusive.
It’s interesting to note the proposed electron structure in context of an atomic orbital. The first s orbital in a hydrogen atom has an energy of 13.6 eV, or a wavelength of about .46 nanometers. But the measured size of the atom including s orbital is around 1/20 of a nanometer, so quantum interference due to the electron is 10 times too big to determine orbital path. Suppose we use the proton wavelength as an interference wave–it does roughly match the orbital radius. But now the problem is that the proton is a different particle than the electron, it will not quantum interfere! In any event, the Schroedinger equation derivation of orbital path uses electromagnetic charge, or photon exchange, so quantum interference can’t be the cause of orbitals.
Now translate down to the much smaller size of the electron itself. These simple calculations show a scaling problem: quantum interference seems really unlikely to confine the electron wave to a soliton that is much smaller than the hydrogen orbital path, and smaller still than the electron wavelength. We could hypothesize that at the electron size, a dipole would orbit at relativistic speeds to allow very high frequency quantum interference waves to confine the orbit path, but this isn’t really anything other than pure speculation.
In spite of all this, quantum interference analysis should still be a theoretical basis for the electron structure experiment–the scale problem doesn’t invalidate the strategy for inferring internal structure. We just have to find a way it can be done in a practical lab environment. If it could be done, that would just be the beginning of learning how to use measurable quantum interference patterns to probe deep into the structure of all subatomic particles. I see an analogy in the X-ray crystallography method.
Separate from all that–to me it’s an interesting curiosity that quantum interference should produce a soliton wave solution. I wonder if this actually does show up in nature in some different way that I don’t see yet.
end of UPDATE
In previous posts, I have proposed several ways to determine subatomic particle structure using quantum interference. One such structure question is whether the electron is a monopole that oscillates or twists in place, or is a dipole consisting of two nodes that orbit around each other. I came up with a tilted two-slit experiment that should allow finding which structure matches reality.
However, one problem with this tilted two-slit experiment described in the previous post is the need to figure out what interference pattern corresponds to the monopole (concentric circle) and dipole (spiral) wave patterns. While some computation or calibration could be done to make the experiment work, I realized there is a much better way to do this.
With a great Aha moment, I realized nature has already provided us with the means to distinguish the two cases. There are four particles including the electron that will quantum interfere: the spin-up electron, the spin-down electron, the spin-up positron, and the spin-down positron. If the wave pattern derives a spiral from the dipole case, the four cases will spin in opposite direction spirals relative to the particle moment. If the particles derive a concentric circle pattern from a monopole, you should get the same wave pattern regardless of particle type.
There will be two pairs of particles with the same wave pattern (the spin-up electron with the spin-down positron–and the spin-down electron with the spin-up positron). Set the two-slit apparatus tilt for Pi/2 phase offset tilt off vertical (I computed this tilt as offset_angle = arccos(1/4 * 1.1 nm / 7 nm), or about 2.5 degrees, for a 7 nanometer two-slit barrier). Now shoot sets of particles from one or the other pair at the barrier (see the figure).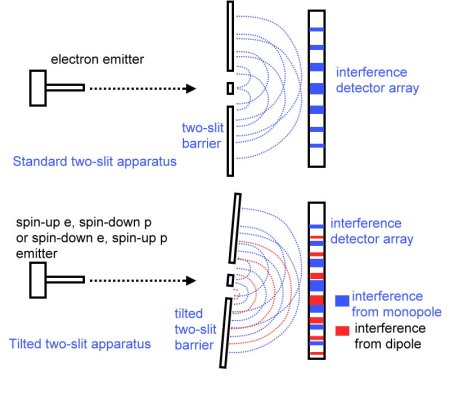
If you get two distinct interference patterns, one for each pair, the conclusion is unmistakable–the particles have a spiral wave pattern and form from a dipole. If the pattern is the same for all particles, they have concentric circle wave patterns and form from an oscillating or twisting monopole.
Anybody want to make me a 7 nanometer two-slit barrier apparatus? 🙂
Agemoz
Tags: fermion, physics, quantum, quantum interference, subatomic particle, two-slit experiment
Agemoz's Physics Blog 
Leave a comment