UPDATE: improved the listed Mathematica code by setting up a Fourier delta function sum to make the constant velocity easier to see, adding better comments, and showing a better view of the functions using different frames of reference.
2ND UPDATE: Fixed missing velocity vr term in Mathematica formula. 3RD UPDATE… arggh, that update wasnt right.. fixed now with matching units. The result where different vr (frame of reference velocity) values result in constant v0 speed is correct. And–one last update to the Mathematica code that adds a negative reference frame velocity–this shows the robustness of the theory, it still maintains constant observed velocity v0 in spite of different observer velocities vr. I updated the pictures to show this new result.
The theory of special relativity is built on the assumption that the speed of light (in a vacuum) is constant. I wrote a proof of a theory why reality has this constant speed:
This derivation shows that in classical physics, any entity composed entirely of waves in spacetime will always appear to be moving at a fixed speed regardless of the observer’s frame of reference relative velocity. If we accept this statement as applying to reality, it should be a logical deduction that as all particles and fields in our reality obey special relativity, they must all be composed entirely of waves in spacetime. If any component internal to a particle is not constructed of waves, it will not Doppler shift, and its velocity will sum with the velocity of the observer’s frame of reference, causing it to disassociate from the rest of the particle.
Why do I mention this now in the midst of my ongoing work on the nature of quantum decoherence (see previous post, where I determine that decoherence cannot be mediated by a spacetime field between entangled particles)? The Standard Model cannot help us resolve what actually happens, but this paper shows there must be a wave basis for all particles. If we also use the accepted knowledge that quantum decoherence is a quantum wave effect (quantum states are represented mathematically as wave functions), we obtain a step forward on the path to resolution.
The paper specifies that a classical physics Fourier sum of waves will always produce an observed constant speed regardless of the observer’s frame speed. Since this conclusion is new (not part of established physics for reality) it is worth understanding why this works in depth, which is why I wrote a mathematical proof. It’s possible to set up a simple geometric simulation using classical Doppler shifting. I set up a very basic Mathematica animation that demonstrates the principle proven in the paper for different frames of reference velocities. You can run it with the simple code I show here:
UPDATE: improved code that ensures that apparent constant speed is observed in one animation, otherwise it’s possible different animations could possibly run at different speeds). Fixed incorrect unit matching in equations.
(* create a Fourier component in spacetime, moving at velocity v0.
Offset it in the y direction for visibility. v0 and vr point in
the positive x direction. While the ability to use a time-varying
particle is provided, this illustration assumes a delta function
in space only (easier to see the constant speed result) *)
comp[x_, t_, k_, f_] := Sin[2 Pi (k x - f t)]
(* Here is a Fourier composition wave that forms a delta function *)
ftd[x_, t_, k_, f_] :=
comp[x, t, k, f] +
comp[x, t, 2 k, 2 f] +
comp[x, t, 3 k, 3 f] +
comp[x, t, 4 k, 4 f] +
comp[x, t, 5 k, 5 f]
(* doppler shift the ftd Fourier composite delta function in
space depending on the observer's frame of reference speed. Also,
move x by the frame of reference speed vr. The theory (basis for
wave based particles having a constant speed comes from these
two factors cancelling out, leaving only the original v0. *)
dsftd[vr_, v0_, x_, t_, k_, f_] := ftd[x-vr, t, v0/(v0 - vr) k, f]
(* Now plot several frames of reference speed to demonstrate the
constant speed of the delta function for each vr (velocity of
reference frame). Note an arbitrary constant y is added to the
plots to allow visibility of combined plots. *)
plotdsftd[vr_, v0_, t_, k_, f_, y_, c_] :=
Plot[dsftd[vr, v0, x, t, k, f] + y, {x, 0, Pi},
PlotPoints -> 200, PlotStyle -> RGBColor[c], PlotRange -> {-4, 30}]
(* to emulate the observer frame of reference, move the emitter
(and the emitted wave) by some frame of reference speed vr set
from the emitters point of view, the velocity of the wave causes
a constant phase shift over time. Doppler shift the spatial
frequency of waves by 1/vr. In addition, move the observer's
frame of reference (x offset) by vr times t. You may have
to slow the animations down. Now observe that all velocities
are the same regardless of the observer's frame of reference speed. *)
plotdsftd[0, 0.5, 0, 1, 1, 0, {1, 0, 0}]
ar = .4
(* Show wave sums, each of four different frames of reference
velocity. Observer will see the delta function move at a
constant speed regardless of the frame of reference velocity *)
Animate[Show[plotdsftd[0, 1, t, 1, 1, 0, {0, 0, 0}],
plotdsftd[-0.3, 1, t, 1, 1, 6, {1, 0, 0}],
plotdsftd[-0.5, 1, t, 1, 1, 12, {.5, 0.5, 0}],
plotdsftd[-0.8, 1, t, 1, 1, 18, {0, .6, 0}],
plotdsftd[0.2, 1, t, 1, 1, 24, {0, .6, 1}]], {t, 0, 10, .03},
AnimationRate -> ar]
Here are pictures:

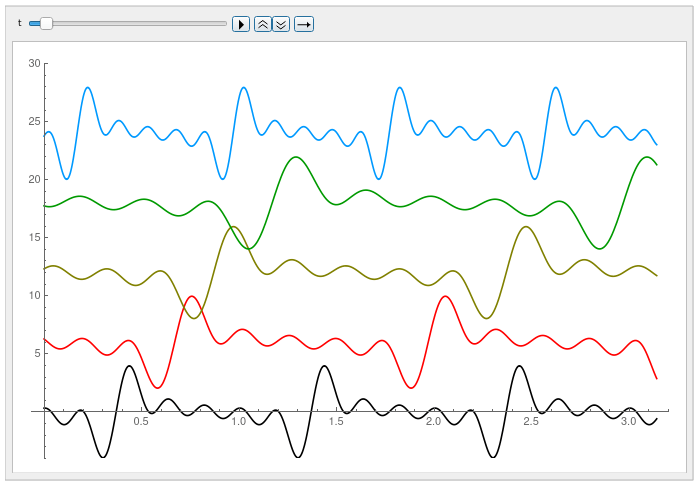

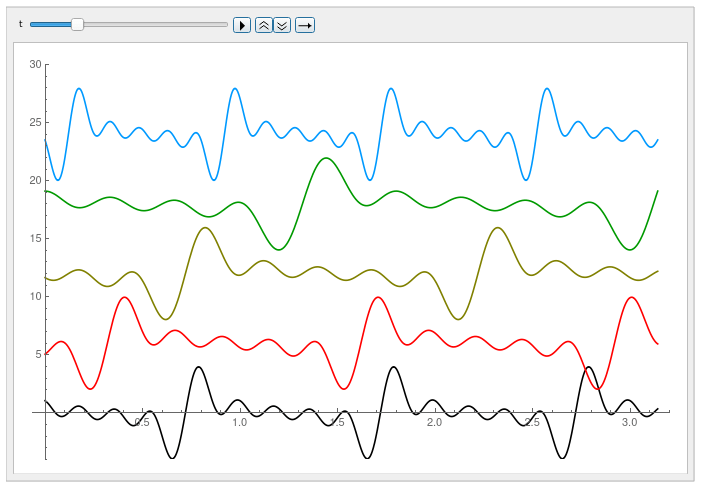
The examples are all running with different observer’s frame of reference velocities (black=1.0,red= 0.8, brown=0.5, green=0.2, blue=-0.2), yet all are moving at the same velocity. This is a nice demonstration of what I proved in the paper–that objects constructed of waves always appear to move at the same velocity regardless of the observer’s frame of reference velocity.
This is why I strongly believe that reality has the constant speed of light that underlies the principles of special relativity. Note that once you have a constant speed, it is easy to show geometrically that this results in time and spatial dilation by the beta factor used in special relativity–many have done this, and I refer you to papers on Arxiv and other places. Currently, the Standard Model does not postulate a cause for the constant speed, it is one of two assumed postulates that are the foundation for the theory of special relativity. By finding an underlying cause for this postulate, I think we now have a valuable tool for making progress understanding why quantum mechanics, in particular, quantum decoherence and quantum interference, exists. Since all particles can only have wave components, a variety of approaches become available for study, which I will do in following posts.
Agemoz
Tags: physics, quantum, science, special relativity
Leave a comment