Electrons come in four variations: spin-up e-, spin-down e-, and their antiparticles, spin-up p+ and spin-down p+. They all are, to the best of our knowledge, point particles and have precisely the same mass and charge magnitude. Throughout the history of physics, DeBroglie and many others tried to create dipoles and other (non-point) configurations to explain these variations but all fail to match experimental observation.
Point particles are a difficult model to work with geometrically in 3D space (R3)–there’s few properties you can assign to a point particle that would model the four electron variations. Even geometric spin is a questionable attribute unless the particle is assigned spin in the limiting case as the radius goes to zero. Even in that spin case in R3, there is no way to get the four variations just from spin because we must observe gauge/frame of reference invariance. You can’t even get two variations in R3! There’s always an observer transform (rotation or displacement) that will transform any given spin orientation in R3 into any other possible spin orientation. In R3, you only can have one electron variation, not the four that we observe.
The R3 + I case is a completely different situation. Point particles do really interesting things in R3 + I!
In the previous post, I make a case that rotations in R3 plus an additional background state rotation direction orthogonal to R3 enables both particle quantization and continuous field twists. It also opens up a completely different–and really interesting–situation on point particle spin. I discovered that there are exactly four possible unique combination spin cases that are topologically distinct and thus are gauge invariant–you cannot perform a rotation, for example, to turn a particle from a spin up case to a spin down case. We can cover the four electron variations in R3 + I!
Here’s an explanation: The first thing to note is that this won’t work in R4 (four dimensions) unless one of them is a background state +I. That is, for this scheme to work, you have to have R3 + I. To quantize rotations, there has to be a preferred (lowest energy) rotation state that I label as +I (see the previous post for more on this). This assignment is also necessary to get four unique spin cases. If you have this +I background state, then you can anchor a rotation about it in either the clockwise or counterclockwise direction. These rotations are topologically unique–you cannot transform one into the other by rotating or otherwise moving the observer. This spin state consumes two of the three dimensions in R3, and I will call this set of spin states S0.
For any rotation position in this R2 + I (S0) case, you can use the third R3 dimension to add an additional orthogonal rotation, let’s call it S1. By itself, S1 isn’t helpful, because the S1 spin cases will not create a unique new spin state for the point particle–the apparent spin will go from clockwise to counter clockwise just by moving the observer to the opposite side along the current S0 direction. However, I discovered that the S0 spin path provides an anchor for S1 because it is spinning–the crossproduct of the R2 + I spin axis S0 rotation direction with the rotation using the third dimension from R3 (S1) will be unique and frame-of-reference invariant in four possible ways. R3 + I thus has four possible point particle variations that would model the spin-up and spin-down e- and p+ elementary particles.
Here I attempt to show a picture of S0 and S1–since I’m representing four dimensions on a two dimensional projection, this will take a bit of imagination to work out what I am trying to show.
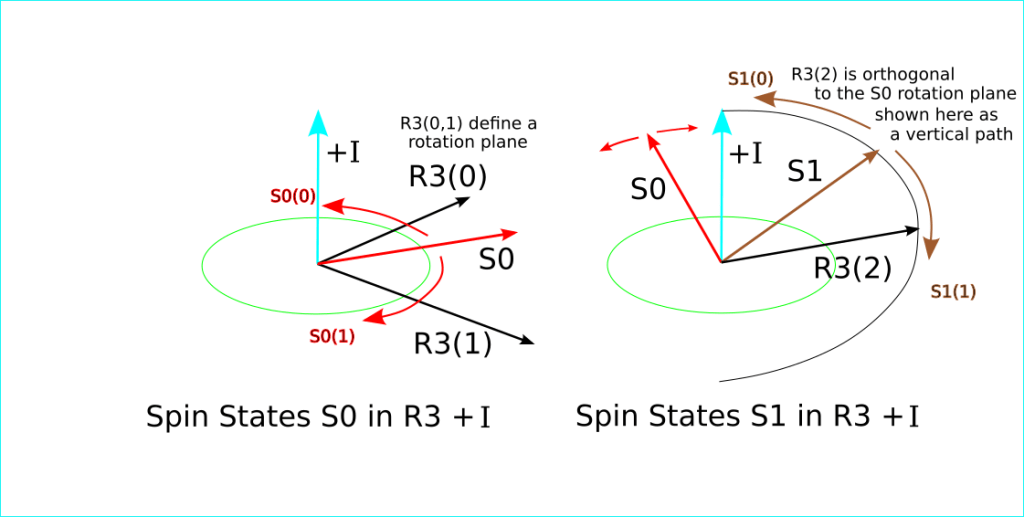
In conclusion–point particles aren’t very useful for modeling elementary particles in R3, but in R3 + I, they lead to a very different and interesting situation. R3 + I can exactly represent (no more, no less) the four unique spin cases that model the four electron variations: spin-up e-, spin-down e-, spin-up p+, and spin-down p+.
Agemoz
Tags: physics, quantum, quantum theory, special relativity
Leave a comment