I’ve always been amazed and intrigued by the universe’s vast array of electrons (and other particle types) that all have precisely the same rest mass, magnetic moment, and quantum interference wavelength. As I discussed in the previous post, the constants are exact regardless of location in space or time, of observer relative frames of reference, presence within electromagnetic fields, and even of gravitationally induced spacetime curvature. I’ve tried to come up with any geometrical construction that would convey this constant behavior over all spacetime, and ruled out any pure geometrical construct that would do this. I also ruled out any scheme dependent on the constant speed of light–in fact, I was able to convince myself that this could not come from any internal property of the activation layer, our current time slice called a 3D hyperspace in 4D spacetime. The only workable hypothesis is that these constant properties of particles are invoked upon creation, that is, when the probability in the creation operator in quantum field theory generates a path to a particle-antiparticle pair.
However, as I showed in the previous post, the creation operator needs to be constrained to provide a quantized particle (quantizing to a specific rest mass, for example), and I hypothesized that nature really only provides one way to do this, via a rotation that has a background state. We see this kind of behavior when looking at atomic orbitals, where the probability distribution must be continuous and thus only allows these quantized states–integer fractions of the time to follow one orbit, one complete rotation. This doesn’t really work the same way for point particles like the electron, though, and while it is clear that this quantization has to occur during the activation of the quantum creation operator, I had to come with new ideas how this could work for point elementary particles.
I believed that the quantized rotation is a big part of why the resulting elementary particles have a constant set of properties no matter where in spacetime the creation operator probability activates, but with no constraint on how long the creation process takes, it seemed like even a quantized rotation could not fully define the particle wavelength and hence mass. We see this in photons–any possible wavelength can result depending on the transition times between atomic excitation levels. It seemed like any possible mass could result from a creation operator activation, and thus electron creation could not explain the constant electron rest mass we see through all of spacetime.
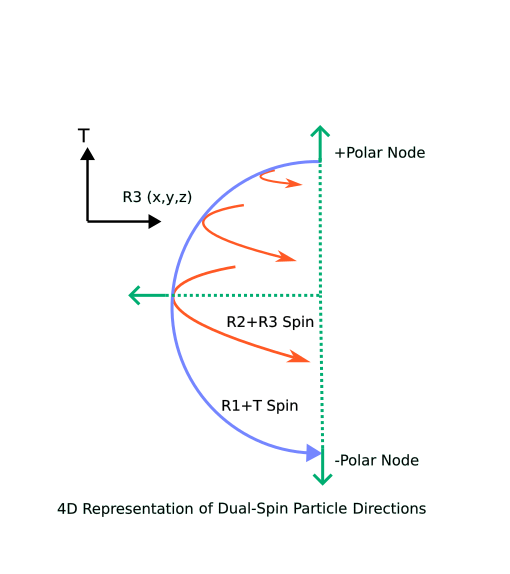
A really nice clue comes from the magnetic moment of the electron. We are taught in physics class not to take spin literally for quantum particles, but I’ve always been disturbed by the magnetic moment paradox of elementary particles. Moments are proportionate to the radius of the center of mass times the angular rotation rate. However, elementary particles have essentially zero radius, so no finite angular rotation rate will give anything but a zero angular momentum. I suddenly realized, here was how the creation operator could produce an absolutely constant mass for the electron no matter where or when it occurs in the universe. The angular rotation rate is infinite! That is, the creation process produces a single complete rotation of a point particle in zero time. Now the radius times angular rate can produce a finite value, and now we don’t need to include passage of time to get the particle rest mass from the creation operator activation.
We aren’t done yet, though, there’s still some issues with this thinking. First, if the rotation rate is infinite, then how do we get the particle’s quantum wavelength? For this, you can go back to previous posts on this website how I propose explaining the apparent non-causal behavior of entangled particles or the dual slit paradox. In the case of entangled particles, the detection of one particle instantaneously enforces the complementary state detection of the other particle. In the dual slit paradox, a particle going through a barrier with two slits will cause an interference pattern on a target detector screen, such that there are places on the screen where the single particle will never go. But close one of the slits, and now the particle can go there. You can time this closing such that there is not enough time for the closing to affect the path of the particle, and yet we still get the corresponding presence or absence of interference region particle detection.
These experiments have caused all kinds of discussions and interpretations such as the EPR (Copenhagen) interpretation, Everett many worlds, and the two variations of the Bohm pilot wave approach. I have long since believed in a new interpretation that no-one else appears to have proposed. This interpretation provides a useful means for understanding the particle-antiparticle creation I’ve been discussing.
In this proposal, particles are group wave constructs. The group waves propagate instantaneously but the phase change of these waves are limited by the speed of light. This means that interference effects such as demonstrated by entangled particles or the dual slit experiment propagate instantaneously, but the particle (the group wave construct) cannot move faster than the speed of light.
Now back to our creation operator activation of a quantized rotation in zero time. The rotation completes in zero time, resulting in a fixed angular moment, but the phase change of this rotation generates the electron particle wavelength. It’s the rotation rate of the background state that sets the quantum interference wavelength (and hence its mass and magnetic moment). I like this idea a lot because it provides not only a means to get the electron constants regardless of spacetime curvature or observer frames of reference, but also provides a definitive answer why we can’t use the DeBroglie or Compton methods for modeling an electron, that is, of wrapping that wavelength around a ring like an atomic orbital–we always knew from experimental evidence that this wavelength was too big to represent any internal structure of the electron. This methodology (retrieving quantum wavelengths of a particle from phase shifting of a zero-time rotation spin rate) is a great explanation for why quantum mechanics works in wave functions and probability amplitudes rather than the math of propagating waves. This electron point particle model at last has a workable geometric construct and gets us much closer to why its properties never vary throughout our universe.
Agemoz