Posts Tagged ‘electron’

« Older Entries

Central Force Charge Infinities

March 26, 2021

In the last post, I stated that if an electron were truly an infinitely small point, and electrostatic fields obeyed the central force relation where force decreases with the square of distance, we should see electrons able to achieve very high velocities. There is an analogy with gravitationally driven masses that slingshot around other masses and gain sufficient momentum to exit the solar system. For example, the P orbital (second excitation state of electrons in an atom) has a probability distribution that intersects with the nucleus, so close encounters should cause large central force acceleration such that the electron would be ejected from the atom at high velocity. We never see this happen for stable atoms, so I concluded that one or more of our assumptions has to be wrong. Either the electron is not a point, or electrostatic fields do not follow the 1/r^2 decrease in strength away from a charge source.

I think enough experiments have been done to show that the bare electron has to be a point as far as we are able to measure. I think trying to find a solution that depends on a significant electron radius is a lost cause.

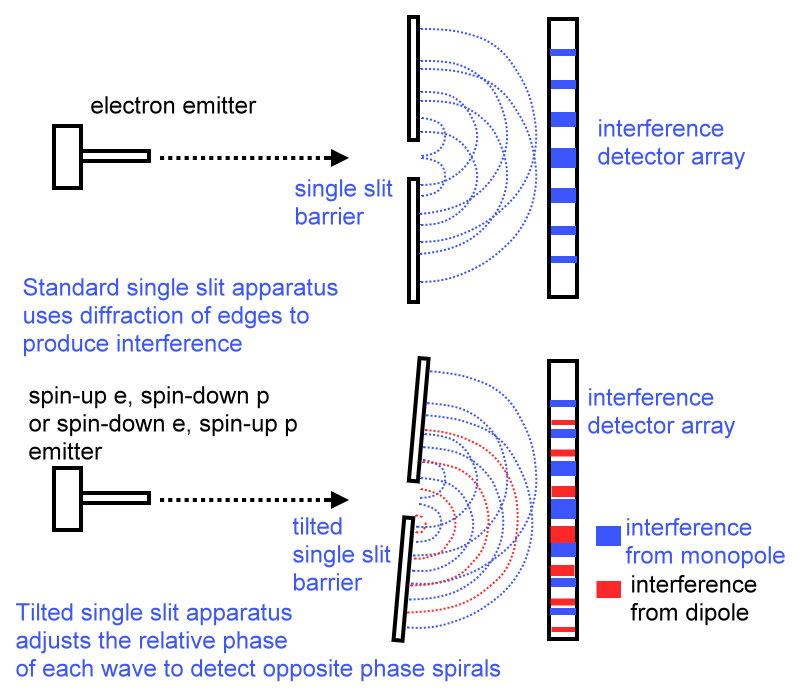
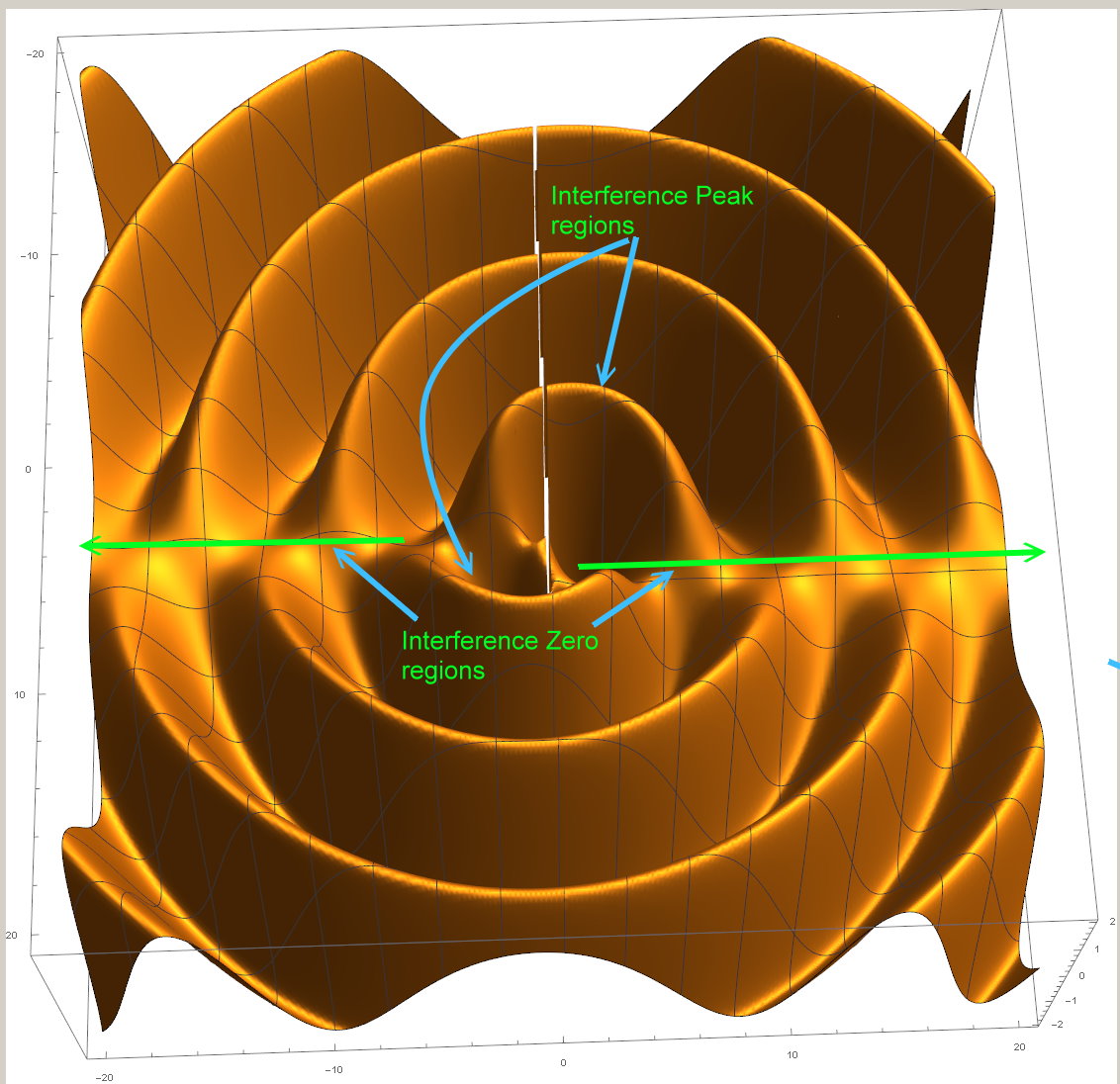
However, I have posted many times working out ideas how the electrostatic field has to be exerted via sinusoidal waves. We already see wave behavior from quantum particle experiments, so I ran several simulations that showed how charged particles are displaced, either as attraction or repulsion, via quantum interference–waves summing to form interference patterns defining particle location probability bands. This led to the hypothesis that charge forces are a consequence of quantum interference, and that the electromagnetic field consists of waves.

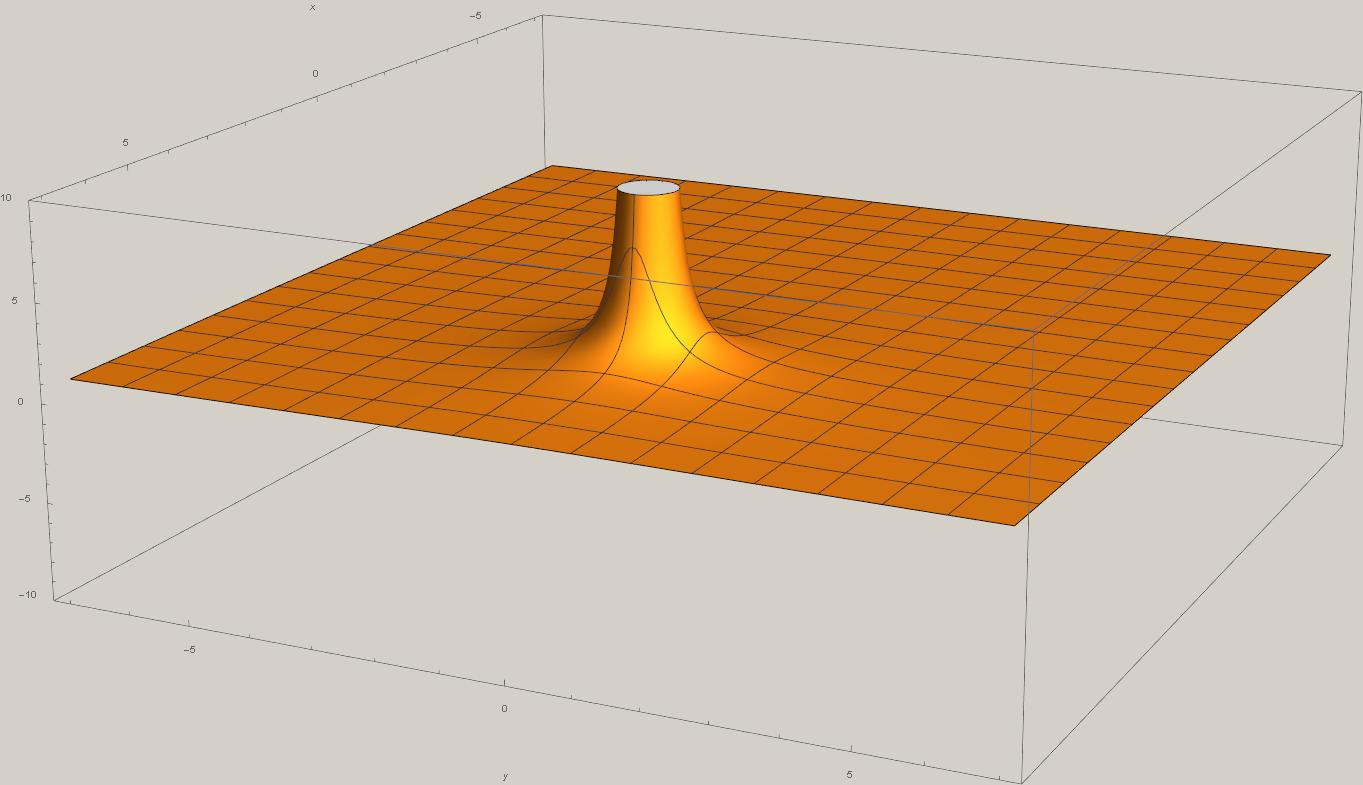
Recently I’ve been questioning why quantum field theory has to use renormalization to cancel out infinities caused by the central force behavior of electrostatic fields. This (and the gravitational mass analogy positing spontaneous expulsion of electrons from atoms) has led me to think that modelling the field as a 1/r^2 central force field is incorrect. I conclude that the electrostatic field near a point charge has to be represented by a probability amplitude, not of 1/r (which would yield a probability distribution of 1/r^2), but must also include its wavelike nature. This means that the probability amplitude would be a sync function: Sin[r]/r, giving a probability distribution of Sin^2[r]/r^2. Now we should not need to renormalize, and we also would no longer have the possibility of electron expulsion from an atom. We still retain quantum properties such as the wavelike interference behavior of particles, but will no longer have infinities caused by a pure central force field.

Agemoz

Tags:, , , ,
Posted in Physics | Leave a Comment »

Electrons and Charge Central Force Equation

March 21, 2021

The Standard Model describes probability distributions for particle motion and interactions, but does not tell us why we have the particle masses and charge forces we can experimentally observe. I’ve found two concepts that can be tacked on to the model–the proof that particles that experience the properties of special relativity have to be composed entirely of waves (see the paper referenced below) and that E=hv implies that particle wave components can be modelled as twists in a unitary vector field in R3+I+T (agemoz.wordpress.com/2021/01/23/unifying-the-em-interactions/). I am very certain of the former, and think the latter is the most likely of all alternatives I can think of.

Since then, I have tried to synthesize hypotheses that would result. Previous posts show how I understand the difference between virtual particle and real (on-mass shell, e.g., conserves momentum at any point in time) particles as partial/returning twists and complete quantized twists respectively. I wrote how real photons have quantized twists with angular momentum through the axis of travel, thus providing the polarization degree of freedom.

Electrons are much more difficult because experiment shows they are infinitely small point particles. So many people have proposed variations of the DeBroglie standing wave in a circle using EM fields–but these cannot explain why experiment collisions show the point particle radius is smaller than any measurable constant. I am certain that EM fields cannot work for many reasons (discussed in previous posts) but even a loop in the unitary twist vector field doesn’t explain the unmeasurably small radius of the electron. In order to define the difference between photons, and to explain photon capture by an electron, whether free or bound to an atom, I saw years ago that a twist loop would be a great explanation (photons try to go through the loop center field region, but at the moment of collision creates a momentary standing wave reflection that cancels itself out, causing a transfer of angular momentum to the electron). But this can’t work if the electron is a point particle. I thought of a new reason to dispute the zero electron radius assumption.

Admittedly, the bare electron doesn’t exist in the real world as a point–it is surrounded by a cloud of particle/anti-particle creation/annihilation operators. The problem remains, however–the central force nature of the EM field forces quantum field theory to renormalize out infinite forces arbitrarily close to the electron inside the cloud.

Renormalization is necessary because of the central force nature, the strength of the field varying as 1/r^2, of the EM field–the charge of the electron produces this field which then impedes the motion of the electron to some extent. This field strength asymptotically goes to infinity as you approach the electron, that is, as r goes to zero. If the electron is truly point sized, we have to compute the effect of the field arbitrarily near the electron, and the only way to get non-infinite results reflecting reality is to arbitrarily cancel out the field infinite forces near it.

There’s a really interesting way to look at the central force equation near point particles, and it comes from the behavior of gravitational masses. Gravitational particles can experience infinite central force behavior, or more accurately, forces far beyond the energies present in the local region of the system. Look at the particle jets emitted from spinning black holes–the masses present in the jets are accelerated to incomprehensible velocities. We see the same thing when a spacecraft swings close enough to a planet to give it enormous kinetic energy, sufficient to rocket it out of the solar system like the Voyager spacecrafts.

It suddenly hit me–we do not see this happen with electrons! Even the most powerful collisions at CERN never shows this asymptotic slingshot behavior–the interaction momentums are always conserved. I think we will find answers to the nature of electrons by comparing the two systems. The potential energy near a gravitational mass can become enormous as the radius of the mass gets smaller, but this doesn’t happen for particles! Why not? One thing is for sure–the fact that we see no jets or massively accelerated particles in electron interactions means that the existence of an infinitely small point electron in a central force EM field, the central assumption of quantum field theory renormalization, cannot be an accurate description of reality.

Agemoz

Tags:, , , , ,
Posted in Physics | Leave a Comment »

Properties of a Unitary Rotation Field

January 6, 2020

The unitary rotation field in R3+I dimensions is part of a quantum interpretation that obeys special relativity.   Recently I was able to show that the field can produce both linear and closed loop soliton solutions that do not produce discontinuities in the field.  This is a big step forward in the hypothesis that this field is a good representation of how things work at the quantum/subatomic scale.   Note that this field is NOT the EM field, which under quantum field theory reduces to a system of quantized and virtual particles.

This unitary rotation vector field is derived from the E=hv quantization principle discovered by Einstein more than a century ago.  This principle only allows one frequency dependent degree of freedom, so I determined that only a field of unitary twists of vectors could produce this principle.  (I didn’t rule out that other field types could also produce the principle, but it’s very clear that any vector field that assigns magnitude to the vectors could not work–too many degrees of freedom to constrain to the E=hv property).  This has two corollaries:  first, no part of the field has zero magnitude or any magnitude other than unity, and, the field is blocking–you cannot linearly sum two such fields such that a field entity could pass through another entity without altering it.

Why did I determine that the rotation has to be in R3+I, that is, in four dimensions (ignoring time for now)?  Because of the discontinuity problem.  If the field were just defined as R3, you cannot have a quantized twist required to meet E=hv.  No matter how you set up the rotation vectors around a twist of vectors along an axis, there must be a field discontinuity somewhere, and field discontinuities are very bad for any reality based physical model.  That makes the field non-differentiable and produces conservation of energy problems (among many other problems) at the discontinuity.

However, all of quantum mechanics works on probability distributions that work in R3+I, so that is good evidence that adding a fourth dimension I for rotation direction is justified.  It doesn’t mean there is a spatial displacement component in I–unlike the R3 spatial dimensions, I is just a non-R3 direction.  And the I dimension does at least one other extremely important thing–it provides a default background state for all vectors.  In order for photons and particles to have quantized twists, a background starting and stopping vector rotation is necessary.  The unitary field thus normally would have a lowest energy state in this background state.

Aha, you say–that can’t work, the vacuum is presumably in this lowest energy state, and yet we know that creation operators in quantum mechanics will spontaneously produce particle/anti-particle pairs in a vacuum.  You would be correct, I have some ideas, but no answers at this point for that objection.  Nevertheless, I recently was able to take another step forward with this hypothesis.  As I mentioned, it is critical to come up with a field that does not produce discontinuities when vector twists form particles.  Unlike R3, the R3+I field has both linear and closed loop twist solutions that are continuous throughout.

This was very hard for me to show because four dimensional solutions are tough to visualize and geometrically solve.  I’m not a mathematician (whom would undoubtably find this simple to prove), so I used the Flatland two dimensional geometry analogy to help determine that there are continuous solutions for vector twists in four dimensions.  There are solutions for the linear twist (e.g., photons) and closed loop particles.  There are also solutions for linked closed loops (e.g., quarks, which only exist in sets of two or more).

I will follow up next post with a graphical description of the derivation process (this post is already approaching the TL;DR point).

Now, this is a very critical step indeed–there is no way this theory would fly, I think, if field discontinuities exist.  However, I’m not done yet–now the critical question is to show that the solitons won’t dissipate in the unitary rotation field.  If there are no discontinuities, then the solitons in a field are topologically equivalent to the vacuum field (all vectors in the +I background state).  What keeps particles stable in this field?  As dicussed in previous posts, my hypothesis has been to use the displacement properties of quantum interference–now that the discontinuity problem is resolved, a more thorough treatment of the quantum interference effects on the unitary rotation field approach is now necessary.

Regardless of how you think about my hypotheses that unitary rotation vector fields could represent subatomic particle reality, surely you can see how interesting this investigation of the R3+I unitary rotation field has become!

Agemoz

Tags:, , , , , , , ,
Posted in Physics | Leave a Comment »

Corrected Tilted Slit Experiment

August 11, 2019

CORRECTED UPDATE 19/08/10:  further analysis shows that the proposed experiment isn’t going to work as proposed.  I obtained a 1.1 nanometer electron wavelength for a static electron, but this is wrong.  Unlike photons, fermions have a wavelength that varies as their kinetic energy, but I did this incorrectly.  I recently recomputed the wavelength in a different way, simply by using E=hv.  Using E=.511MeV, or 8.2^10-14 J, and Planck’s constant as 6.6^10^34 J*s, I get an electron wavelength c / v or 2.998 10^8 m/s / 1.2 10^20cyc/s, which gives a wavelength for the static electron as 0.024 nanometers.  This is good news and bad news:  This wavelength now means that quantum interference could be the confining property for solitons, as I originally proposed a few posts back.  The bad news is that making a tilted two-slit experiment is probably not possible–the wavelength of the atoms composing the barrier is twice the length of the electron wavelength, so I think there is no realistic way to make an electron tilted two-slit barrier where the tilt could discern the electron interference pattern.  Since a single slit has two edges which will cause diffraction of the electron wave on both edges, it might be possible to create a barrier of layers of cold solid hydrogen (such a barrier would have to require some sort of atomic sublayer as a base since hydrogen forms only one bond) with a single slit that generates two interfering electron diffraction waves.  Tilting this barrier may be sufficient to discern whether electrons and positrons (or up-spin and down-spin electrons) produce two different interference patterns.  I’m tempted to submit an NSF research grant for such a research project just to see if I get anything besides a desk rejection!

The good news part of it means I want to return to my work using quantum interference as the cause of soliton particle formation.  This corrected wavelength computation now means quantum interference should produce self contained paths.  I do have to assume that any particle such as the electron has to have a dipole (or more) structure, as there will be no interference pattern from a monopole.  Waves, yes, but no interference that will define an orbiting path.  It’s really too bad that the tilted slit experiment is beyond the reach my lab skills and equipment–it would have been great to try to answer whether the electron structure is a monopole (concentric circle waves) or a dipole (spirals or antispirals).  My hunch based on all my investigative work is that it is a dipole, which means that the quantum interference redirection will produce sufficiently small paths to confine the electron waves.  It’s clear to me that investigation is now the way to go.

Stay tuned!tilted_single_slit

Tags:, , , , ,
Posted in Physics | Leave a Comment »

Determining Subatomic Particle Characteristics from its Quantum Interference

July 18, 2019

Edit update 190719: Addendum added see below–another possible experiment

Every subatomic fermion (non exchange particle such as an electron) has a specific mass and hence wavelength, and thus will produce quantum interference with another particle of the same type or with itself.  This quantum interference will cause particle motion to be redirected, for example to specific locations (interference pattern) on a target detector in the two slit experiment.  It seems logical that studying the quantum interference effects of a particle will lead to insights about the particle structure.

In the previous post, I showed how the quantum interference pattern could be used to make a guess about particle internal structure.  It could form a soliton if the particle were a loop whose radius matched the wavelength of the particle.  But, if the particle radius is much smaller than its characteristic wavelength, this doesn’t work and the particle cannot be constructed using quantum interference.  I showed how a ring structure could produce the tiny point collision signature but still produce waves with the particle’s characteristic wavelength.  If we were able to determine if quantum interference forms electron structure, we could answer the size and topology question for once and for all.

But there’s more we can get from quantum interference.  If an electron is truly infinitesimally small, much smaller than the electron characteristic wavelength, we will have no way to determine internal structure by experimental observation.  But we can use its quantum interference pattern, whose characteristic wavelength scale is much much larger, to indirectly figure some things out.

For example, one great question to ask is whether the electron is a monopole oscillating or twisting in place– or consists of two nodes, a positive and a negative node spinning in a dipole orbit.  As far as I know, there is no experimental or theoretical work that determines which is reality for any subatomic particle.  There is no possible way to distinguish these two cases directly if the electron is infinitely small, which is the current physicist consensus.  But these two cases will have different characteristic wave patterns!  The monopole case will produce waves as concentric circles about the center.  The dipole will produce a spiral and will have a radiating peak and zero path.

monopole_down

monopole oscillates in place

monopole_up

monopole oscillates in place

monopole_pattern

monopoles produce a concentric circle pattern

dipole

dipole structure in orbit

interference_well

dipole spiral interference pattern

Admittedly, conducting an experiment that observes quantum interference in this distance range will be problematic at best.  But there’s one more important difference between the patterns generated by monopoles and dipoles that should help:  in a monopole particle, the phase of waves emitted both toward and away from the particle will be the same–but the phase of of spiral waves will be different by Pi/2 (90 degrees).

This characteristic wavelength should be in reach of (very) sophisticated observation apparatus–the electron wavelength, called the deBroglie wavelength, is 1.22 e^-9 meters.   The wavelength of visible light is in the range of 400 to 700 e^-9 meters, but energetic X-rays fall into range of this characteristic wavelength. If we could match the characteristic wavelength with an X-ray emitter (using electron-positron annhiliation, perhaps?), we would see observable interference that would either be the same or different on the leading and trailing particle wave paths, leading to either a monopole or dipole determination.  If such an experiment could be made practical, we should be able to get a significant clue of the internal electron structure even if the electron is infinitesimally tiny!

Do you see why I think quantum interference could be as powerful a measuring tool for science as, perhaps, the LIGO experiment?

Agemoz

Edit Addendum:  It occurred to me that there might be a better way to detect whether electrons have a monopole or dipole structure using a diffraction grating.  Silicon processes for fabricating computer chips are at 7 nanometers–the width of 6 or 7 electron wavelengths, so we are within reach of fabricating an experimental setup for electron emitters.  When computing the expected interference pattern in a two-slit experiment, Huygen’s principle is used.   This principle conforms to the concentric circle pattern that comes from a monopole.  Unfortunately, the current typical two-slit experiment has the barrier device (with two slits) oriented perpendicular to the emitted electron’s path and will not be able to determine which interference pattern is present. The dipole structure will give the same answer as the monopole case, because the wave pattern is sampled by the two-slit apparatus at the same phase point for either of the slits.

However, if the two-slit apparatus is tilted from the normal to the electron trajectory, you will have one of the slits slightly time and space delayed from the other, and now the resulting interference pattern will be dependent on the phase shift that occurs when you encircle the particle.  In other words, the spiral will be distinguishable from the concentric structure, and this experimental setup should point to either the monopole or dipole structure.

Tags:, , , ,
Posted in Physics | Leave a Comment »

Summary of Findings So Far

February 5, 2018

I took the time to update the sidebar describing a summary of the unitary twist field theory I’ve been working on.  I also paid to have those horrid ads removed from my site–seems like they have multiplied at an obnoxious rate on WordPress lately.

One problem with blogs describing research is the linear sequence of posts makes it really hard to unravel the whole picture of what I am doing, so I created this summary (scroll down the right-hand entries past the “About Me” to the Unitary Twist Field Theory) .  Obviously it leaves out a huge amount, but should give you a big picture view of this thing and my justification for pursuing it in one easy-to-get place.

The latest:  I discovered that the effort to work out the quark interactions in the theory yielded a pretty exact correlation to the observed masses of the electron, up quark and down quark.  In this theory, quarks and the strong force mediated by gluons is modeled by twist loops that have one or more linked twist loops going through the center.  This twist loop link could be called a pole, and while the twist rotation path is orthogonal to the plane of the twist loop, the twist rotation is parallel and thus will affect the crossproduct momentum that defines the loop curvature.  Electrons are a single loop with no poles, and thus cannot link with up or down quarks.  Up quarks are posited to have one pole, and down quarks have two.  A proton, for example, links two one-pole up quarks to a single two-pole down quark.

The twist loop for an up quark has one pole, a twist loop path going through the center of it.  This pole acts with the effect of a central force relation similar (but definitely is not identical to an electromagnetic force) to a charged particle rotating around a fixed charge source–think an atom nucleus with one electron orbiting around it.  The resulting normal acceleration results from effectively half the radius of the electron loop model, and thus has four times the rotation frequency and thus 4 times the mass of an electron.  The down quark, with two poles, doubles the acceleration yet again, thus giving 8 times the mass of an electron.

It will be no surprise to any of you that this correlates to the known rest masses of the electron, up quark, and down quark:  .511MeV, 2.3MeV, and 4.8MeV.

I can hear you screaming to the rafters–enough with the crackpot numerology!  All right, I hear you–but I liked seeing this correlation anyway, no matter what you all think!

Agemoz

Tags:, , , , , , , , , ,
Posted in Physics | Leave a Comment »

Simulating the Universe

November 6, 2017

That title is a bit of a tease, although it is what I’m trying to do, at least on some level. I went through a major redo of my physics simulation software because it was based on the Unity environment, which, while easy to get working and makes use of physics intrinsics built into the Unity graphics environment, turned out not to be suitable for my sim runs. Even with a fairly highpowered PC and some level of optimization work, it was too slow and could not realistically process a large enough field array memory. I could have eventually learned enough about Unity to overcome my initial findings, but I am several orders of magnitude off from the performance I needed, so I did a massive learning curve effort and switched to CUDA programming. This turned out to be pretty close to ideal for what I needed, because in the end the physics provided in Unity wouldn’t work anyway–I would have had to write my own physics, never mind the performance and memory limitations. CUDA is turning into a fantastic environment for what I want to do.

This did get me thinking about the big-picture view of what I am doing. I can imagine the overarching intelligent being or beings (either God or real physicists) overlooking what I am doing–“Oh look, a little doofus putzing around on a computer thinking he will find new physics, God and the meaning of existence!” Yup, that’s exactly what I’m doing, although there’s been a huge amount of guided thinking before initiating the sim process.

There has to have been hundreds of thousands of real physicists who have created field sims with various ideas for algorithm kernels and nobody has found something that’s even close to a match for observed science. What makes me think I can do what so many have already tried? Here’s what I think: it’s partly because of what we know of EM field central force behavior. I’m betting that a large percentage of people think the underlying field that gives rise to EM fields, gravity and particles must have central force behavior, and set up field kernels that dissipate over distance. As I’ve noted in a previous post, this cannot work for a bunch of reasons, one of the strongest being that QFT interactions never work this way (all forces are mediated by quantized exchange particles that do not dissipate). So why do EM fields and gravity have central force behavior? It’s not because the underlying field is central force. I discovered several years ago something that’s probably obvious to any physicist–any point source granular emission system will look like a central force system if the far-field perspective is taken. This means that the underlying precursor field has to be far different than the obvious guesses based on experiment.

Some realistic means for providing field quantization must be built into the field kernel for QFT to work. I thought for a long time and realized the only geometric means to get quantization specified by E=hv is to provide a modulus function on the precursor field with a preferred state. What I mean by that is that field elements cannot have magnitude, they can only rotate, and in addition have a preferred “lowest energy” rotation state. This rotation can propagate in either a line or in some system of closed loops, but must have an integer number of turns (or twists, thus forming the name of the theory: Unitary Twist Field). Now, for a particle such as an electron or photon or proton to be stable in our existence (R3), the lowest energy direction must point in another direction dimension than in R3, otherwise our universe would have sampling noise detectable by radio telescopes, the Michelson Morley ether detector, or similar sensors. I arbitrarily point this dimension in the I direction. When I set up this list of constraints on a precursor field, I can analytically show that there are two “wells” of field states that should form stable states and hence solitons in the field. Once I lad locked down the constraints necessary for an underlying field, I was able to develop a field kernel that should give rise to a particle zoo, and then I was ready to set up a sim or see if more analytic work could be done.

I’m guessing that most physicists have access to simulation tools like mine (actually likely far better), but I would be pretty surprised if someone has taken the path I have taken. I am very fond of using the “million physicist tool”–that is, it’s been around 100 years and no smart physicist has come up with an underlying field kernel, so any scheme I come up with *must* be “out-of-the-box” thinking. That is, a good rule for investigations that aren’t worth doing is an investigation that has likely been done by 1 or more of a million physicists. As I said, I suspect a lot of people have gone down various central force paths because of EM and gravitational field behavior–but I discovered years ago that a precursor field cannot be central force, and cannot be linear, along with a bunch of other painfully worked out constraints I just mentioned.

In other words, I don’t think anybody else has been in this room I’m standing looking around in. I see promise here (the two energy wells provided by this field kernel) and am hopeful that a CUDA sim will shine light on it.

Agemoz

Tags:, , , , , , , ,
Posted in Physics | Leave a Comment »

The Mystery of Particle Quark Combinations

July 27, 2017

Whenever I lose my car keys, I look in a set of established likely places. If that doesn’t work, I have two choices–look again thinking I didn’t look closely enough, or decide the keys are not where I would expect and start looking in unusual places.

There is a huge amount of data about quarks and the particle zoo, more specifically the collection of quark combinations forming the hadron family of particles. We have extensive experimental data as to what quarks combine to form protons, neutrons, mesons and pions and other oddities, many clues and data about the forces and interactions they create–but no underlying understanding about what makes quarks different or why they combine to form the particles they do–or why there are no known free quarks.

I could travel down the path of analyzing the quark combinations for insights, but I can absolutely guarantee that has already been tried by every one of the half million or so (guess on my part) physicists out there, all of whom have probably about twice my IQ. This is an extremely important investigative clue–I assume everything I’ve done has already been tried. Like the car keys, I could try where so many have already been, or I could work hard to do something unique, especially in the case of an unsolved mystery like quark combinations.

In my work simulating the unitary twist field theory, I have a very unusual outcome that perhaps fits this category–an unexpected (and unlikely to have been duplicated) conclusion. Unitary twist theory posits that there is an underlying precursor single valued field in R3 + I (analogous to the quantum oscillator space) that is directional only, no magnitude. This field permits twists, and restores to the background state I. Out of such a field can emerge linear twists that propagate (photons) the EM field (from collections of photons) and particles (closed loop twists). Obviously, photons cannot curve (ignoring large scale gravitational effects), so unitary twist theory posits that twists experiences a force normal to the twist radius. The transverse twists of photons experience that force in the direction of propagation, but the tangental twist must curve, yielding stable closed loop solutions.

Now let’s examine quarks in the light of unitary twist theory. In this theory, electrons are single loops with a center that restores to I (necessary for curvature and geometric quantization to work. The last few posts describe this in more detail). Quarks are linked loops. The up quark has the usual I restoring point, and an additional twist point that passes through it which I will call poles. This point is the twist from another closed loop. It’s not possible for this closed loop to be an electron, which has no poles other than I, but it could be any other quark. The down quark is a closed loop with two such poles.

The strong force is hypothesized to result from the asymptotic force that results when trying to pull linked quarks apart–no force at all until the twists approach each other, then a rapidly escalating region of twist crossing forces.

So far, so good–it’s easy to construct a proton with this scheme. But a neutron is a major problem–there’s no geometric way to combine two down quarks and an up quark in this model.

Here is where I have a potentially unique answer to the whole quark combinations mystery. Up to this far I can guarantee that every physicist out there has gotten this far (some sort of linked loop solution for quarks–the properties of the strong force scream for this type of solution). But it occurred to me that the reason a free neutron is unstable (about 15 seconds or so) is because the down quark in the unitary twist version of a neutron is unstable. It does have a pole left over, with nothing to fill it, no twist available. The field element at this pole is pointing at Rx, but there’s nothing to keep it there. It eventually breaks apart–and look at how beautifully the unitary twist field shows how and why it breaks up into the experimentally observed proton plus electron. Notice that the proton-neutron combination that forms deuterium *is* stable–somehow the nearby proton does kind of a Van Der Waals type resolution for the unconnected down quark pole. No hypothesis yet on the missing neutrino for the neutron decay, but still, I’m hoping you see some elegance in how unitary twist field theory approaches the neutron problem.

A final note–while I’m extremely reluctant to perform numerology in physics, note the interesting correlation of mass to the square of the number of poles. It might be supportive of this theory, or maybe just a numerical coincidence.

Agemoz

Tags:, , , , , , ,
Posted in Physics | Leave a Comment »

Renormalization

June 25, 2017

I’m working on the math for the Unitary Twist Field Theory sim. The first sim to run is the easiest I know of, the electron/photon interaction, and if the theory doesn’t yield some reasonably good results, the theory is dead, there’s no point in going further. If that happens, hopefully there will be an indication of how to modify it to make it work, but this will be a defining moment for my work. Just recently, something quite astonishing came out of this work to find the equations of motion for the precursor field of this theory.

In the process of working out the force computations, I’ve been able to winnow down the range of possible equations that will rule the components of the interaction. Note first that the sim I am doing is discrete while the theory is continuous, simply to allow a practical implementation of a computer sim. I can add as many nodes as I want to improve accuracy, but the discrete implementation will be a limitation of the approach I am taking. In addition, forces can be local neighborhood only since according to the theory there is only one element to the precursor field, you can’t somehow influence elements through or outside the immediate neighborhood of an element. The field is also incompressible–you cant somehow squeeze more twist elements into a volume.

To express a twist with all of the required degrees of freedom in R3 + I, I use the e^i/2Pi(theta t – k x) factor. Forces on these twists must be normal to the direction of propagation–you can’t somehow speed it up or slow it down. Forces cannot add magnitude to the field–in order to enforce particle quantization (for example E=hv) the theory posits that each element is direction only, and has no magnitude. I use the car-seat cover analogy–these look like a plane of wooden balls, which can rotate (presumably to massage or relieve tension on your back while driving), but there is no magnitude component. The theory posits that all particles of the particle zoo emerge from conservative variations and changes in the direction of twist elements. To enforce rotation quantization, it is necessary that there be a background rotation state and a corresponding restoring force for each element.

In the process of working out the neighborhood force for each field element, I made an interesting, if not astonishing, discovery. At first, it seemed necessary that the neighborhood force would have a 1/r^n component. Since my sim is discrete, I will have to add a approximation factor to account for distances to the nearest neighbor element. Electrostatic fields, for example, apply force according to 1/r^2. This introduces a problem as the distance between elements approaches zero, the forces involved go to infinity. This is particularly an issue in QFT because the Standard Model assumes a point electron and QFT computations require assessing forces in the immediate neighborhood of the point. To make this work, to remove the infinities, renormalization is used to cancel out math terms that approach infinity. Feynman, for example, is documented to have stated that he didn’t like this device, but it generated correct verifiable results so he accepted it.

I realized that there can be no central (1/r^n) forces in the unitary twist field (this is the nail in the coffin for trying to use an EM field to form soliton particles. You can’t start with an EM field to generate gravitational effects–a common newbie thought partly due to the central force similarity, and you can’t use an EM field to form quantized particles either). Central force fields always result from any granular quantized system of particles issued from a point source into Rn, so assuming forces have a 1/r^n factor just can’t work. The granular components don’t dissipate, after all, where does the dissipated element go? In twist theory, you can’t topologically make a twist vanish. Thus the approximation factor in the sim must be unitary even if the field element distance varies.

Then a powerful insight hit me–if you can’t have a precursor field force dependent on 1/r^n, you should not need to renormalize. I now make the bold assertion that if you need to renormalize in a quantized system, something is wrong with your model. And, of course, then I stared at what that means for QFT, in particular the assumption that the electron is a point particle. There’s a host of problems with that anyway–in the last post I mentioned the paradox of an electron ever capturing a photon if it is a point with essentially zero radius. Here, the infinite energies near the point electron or any charged point particle have to be managed by renormalization–so I make the outrageous claim that the Standard Model got this part wrong. Remember though–this blog is not about trying to convince you (the mark of a crackpot) but just to document what I am doing and thinking. I don’t expect to convince anyone of this, especially given the magnitude of this discovery. I seriously questioned it myself and will continue to do so.

The Unitary Twist Field theory does not have this problem because it assumes the electron is a closed loop twist with no infinite energies anywhere.

Agemoz

Tags:, , , , , , , , ,
Posted in Physics | Leave a Comment »

Preparing First Collision Sim

June 22, 2017

I’ve been working fairly consistently on the simulation environment for the unitary twist field theory. I’m getting ready to set up a photon/electron collision, modeled by the interaction of a linear twist with a twist around a loop. The twist is represented by e^I(t theta – k x), yes, the same expression that is used for quantum wave functions (I’ve often wondered if we’ve misinterpreted that term as a wave when in fact the math for a twist has been in front of our noses all along).

This is a great first choice for a collision sim because in my mind there’s always been a mystery about photon/particle interactions. If the electron is really a point particle as the Standard Model posits, how can a photon that is many orders of magnitude larger always interact with one and only one electron, even if there are a gazillion electrons within one wavelength of the photon? The standard answer is that I’m asking the wrong or invalid question–a classical question to a quantum situation. To which I think, maybe, but quantum mechanics does not answer it, and I just get this sense that refusing to pursue questions like this denies progress in understanding how things work.

In twist theory there appears to be an elegant geometrical answer that I’m pretty sure the simulation will show–counting my chickens before they are in my hand, to be sure–the downfall of way too many bright-eyed physics enthusiasts. But as I’ve worked out before, the precursor twist field is an incompressible and non-overlapping twist field. If the electron is a closed loop of twists, and within the loop the twists revert back to the I direction (see previous posts for a little more detailed description), then any linear twist propagating through the loop will add a delta twist to some point in the interior of the loop. Since you cannot somehow overlap twists (there’s only one field here, you can’t somehow slide twists through each other. Each point has a specific twist value, unlike EM fields where you linearly combine distinct fields). As a result, the twist of the loop can unwind the linear twist going through it, causing the photon to disappear and the close loop will pick up the resulting linear twist momentum. This isn’t really a great explanation, so here’s a picture of what I think will happen. The key is the fact that the precursor field has one twist value for every point in R3. It’s an incompressible and unitary field–you cant have two twist values (or a linear combination–it’s unitary magnitude at every point!) at a given point, so the photon twists have to affect the twist infrastructure of the loop if it passes through the loop. It really will act a lot like a residue inside a surface, where doing a contour integral will exactly reflect the number of residues inside.

At least that’s what I think will happen–stay tuned. You can see why I chose this interaction as the first sim setup to try.

Agemoz

Tags:, , , , , , ,
Posted in Physics | Leave a Comment »

« Older Entries