Posts Tagged ‘interpretation’

Instantaneous Quantum Wave Phase Derives Special Relativity

August 24, 2019

None of the current well known quantum interpretations are satisfactory–they all have shortcomings that cause logical contradictions to known experimental data.  I think all would agree that the Everett many worlds interpretation has an element of absurdity to it (doesn’t mean it’s wrong, just seems improbable), and the Copenhagen interpretation where decoherence occurs somewhere near a detector has significant logical problems (see the EPR paradox to start).  Physicists seem to like best the modified Bohm interpretation that works around Bell’s inequality, but it adds a wave term (the guiding pilot wave) to equations describing time evolution of particle position and motion.  This redirects the particle to form an interference pattern on a target–but in so doing, since the particle has momentum, it exerts a force for which we have no experimental evidence.

So, I thought long and hard and came up with a new quantum interpretation that seems to overcome these problems, and as far as I can tell, seems logically consistent.  Better yet, particles that conform to the assumptions of this interpretation must meet the constraints of special relativity.

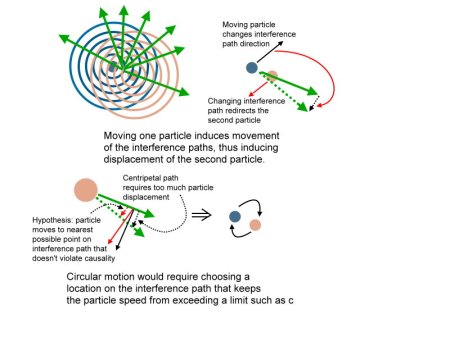
I thought this interpretation flows logically out of the thought process of how quantum interference works.  We know that quantum entangled particles will always resolve to opposite states instantaneously across any distance, appearing to disobey causality (when a detector resolves one of the particles, that sets the state of the other particle instantaneously even if they are far apart–see various Aspect experiment variations).  But, neither particle can exceed the speed of light, nor can any communication between the particles exceed the speed of light.

Now that gives a powerful hint of what this implies–that if the momentum aspect of the particle cannot exceed the speed of light, something else must exceed it.  I realized that if the particle was represented by some construct of waves, the waves could form a rogue-wave–a soliton or delta function where the group could not exceed the speed of light, but component wave phases would not have such a limit–a change in phase would be reflected across the entire length of the wave instantaneously.  The rate of change in time of this phase is limited, so that makes the particle as a whole causal–but the instantaneous effect of this phase change would cause an instantaneous effect on quantum interference over the entire distance of the wave.  And–a quantum interference effect would relocate the particle by virtue of the delta function sum of interfering waves, without the expenditure of energy (the problem with the Bohm interpretation).

This got much, much more interesting as I started working on the math for such a particle–I almost accidentally discovered that such particles would always look like it was moving at the same speed, regardless of how fast an observer was moving!  Instantly, I realized that this quantum interpretation would derive the primary postulate of special relativity–and leads to some pretty astonishing conclusions.  This happens because unlike a solid baseball, a group wave will classically Doppler shift according to the observer’s relative velocity.  If the entire wave Doppler shifts simultaneously, which will be true with this quantum instantaneous phase wave interpretation, the relative velocity of the observer’s frame of reference is exactly cancelled out by the corresponding Doppler shift of the particle’s wave components.

To me, this was an incredibly important finding–it says that any particle formed from instantaneous phase waves will act according to special relativity.  And–if a particle obeys special relativity, it must Doppler shift–and thus must be composed only of various types of wave.  There cannot be any internal structure in an electron, for example, that doesn’t Doppler shift and thus it must be composed solely of wave components.  Now, admittedly, that’s a pretty big box of components–they don’t have to be planar waves, but could be oscillating vectors, helical waves, compression waves, you name it.  All it has to do is Doppler shift and special relativity will fall out.

Amazing! Or so I thought.  I proposed this to many different experts in this field, and all of them pooh-poohed it.  I submitted to 5 journals–all rejected.  I guess I’m totally on my own, which is rather a shame–I think there’s some really good new stuff here.

Agemoz

PS: here’s the mathematical derivation, feel free to comment:

group_wave_constant_speed

Tags:, , , ,
Posted in Physics | Leave a Comment »

Quantum Interference Defines a Soliton

June 18, 2019

In my last post, I described a quantum interpretation based on group waves with an instantaneous wave phase property, and showed how it derives a constant speed regardless of an observer’s frame of reference, setting the stage for special relativity.  I also showed how it would resolve the EPR (Einstein-Podolsky-Rosen) paradox for entangled particles in the Aspect experiment cleanly without adding some unknown force.  This is a flaw with the Bohm interpretation, among others, since it means that work is done and energy expended, causing a conservation of energy violation.  We do not need to believe in multiple parallel universes (Everett interpretation) or try unsuccessfully to create a logically consistent causality using the Copenhagen interpretation.

I then showed how a instantaneous phase group wave particle could self-interfere in the two-slit experiment to logically explain the target interference pattern distribution.  In this explanation, I show the very nature of the group wave will cause particle displacement due to the summation of interfering wave components.  No pilot wave guiding, with its implied force and consequent work and energy expended, is needed.

I suddenly realized that the group wave quantum interpretation provides a possible approach for creating a soliton–a particle could form in a system based on this quantum interpretation.

For over a century, theoretical researchers have guessed that the particle zoo (the list of subatomic particles that make up protons, atoms, exchange forces, and so on) could form from a continuous field (lattices, i.e., discrete fields, have been ruled out at this time both experimentally and theoretically).  DeBroglie was one of the earliest well known scientists that worked with this idea, but Compton and others also came up with proposals.  Early efforts assumed that solitons might form from an electromagnetic field via some selected arrangement of charge distribution, but EM fields and particles have the central force property F = c_0 q_1 q_2/(r^2), and by Maxwell’s field equations behave linearly, so basing particle existence on an EM field was disproved–particles would dissipate.  If there is a field underlying formation of particles, it cannot be electromagnetic, but rather an underlying “precursor” field from which EM fields could emerge.  Dirac’s work led the way to the modern quantum field theory, which further ruled out an EM field creating solitons–EM fields consist entirely of collections of real and virtual photons that travel in straight lines (ignoring space curvature from general relativity at quantum scales).

But instantaneous phase group wave theory can form solitons.  No matter what quantum interpretation you believe in, you have to face the fact that a single particle going through two slits is going to experience redirection when you open one of the slits.  The fact that this redirection happens means that at some scale, a particle will curve in on its path–it must follow the interference pattern.  I have found a variety of ways that a moving interference pattern will circulate or follow more complex loop variations.  For the same reason that the two-slit setup forms an interference patterned domain of existence for a particle, the appropriate pair (or more) of particles will self interfere to form stable loops.  Follow the interference and you will describe a variety of possible particle paths.

Does this reflect reality–dunno, but work is ongoing.  I’m coming up with a mathematical toolset that will describe various interference path constructions.  I will follow the yellow brick road and see where it leads…interference_path_soliton

Agemoz

Tags:, , , ,
Posted in Physics | Leave a Comment »

Why Does Quantum Interference Affect Particle Path?

June 11, 2019

I last posted on my discovery that any classical group wave will obey the observed constant speed property, a prerequisite (one of the two assumed postulates) for special relativity.  That is, if you throw a baseball, its speed will be some value v_p.  If you are standing on a train moving in the same direction at speed v_e, an observer on the ground will see the baseball move at speed v_p + v_e.  But, if you throw an object that is a linear sum of waves, such as a delta function group wave, it doesn’t matter what v_e (the relative speed of the thrower) is, the observer on the ground will always see it move at speed v_p.

The math and concept seemed bullet-proof, so I spent a couple of years writing a paper and trying to get it published.  I stayed away from any speculation and just wrote a proof that says classical group waves must appear to move at some constant speed v_p regardless of an observer’s frame of reference velocity v_e.  I made sure there was nothing in there that would make a reviewer immediately toss the paper.  I worked on getting the format and grammar acceptable for scientific publishing, had several reviewers check it for errors and conceptual problems.  They claimed it was good to go so then I submitted to several journals.  No luck–a bunch of rejections later and I finally gave up.  However, no editor wrote to disprove my math or the conceptual thinking, not sure they ever looked at that–it was always the paper doesn’t meet the quality standards of the journal or some such reason (if any).  In spite of my best skeptical analysis, I cannot find fault with the derivation, and I still think there’s some science here, so I decided to forget the publishing effort and just continue seeing what I could discover on my own.

Here it is: group_wave_constant_speed

Unlike many of the ideas I post here, which are guesses how things work and are borderline science fiction, I thought this work was a small breakthrough, it says several important things.  First, if this is true (represents reality), it shows why special relativity exists in our universe.  All the research I have done shows that no one has determined why we assume the constant speed of light postulate holds and thus why we have special relativity behavior.  Second, it shows that every particle and exchange particle must consist entirely of some kind of a wave summation, otherwise it would violate special relativity–thus giving an important clue how to mathematically define subatomic particles.  And third, it shows that any quantum particle composed of waves must phase shift the waves at a causal rate–but there can be no time-dependent component to the phase-shift along the length of the wave.  In other words, the entire wave component shifts non-causally, albeit at a causal rate.  This is important because now the Aspect experiment makes sense–if entangled particles are emitted in opposite directions, the particles stay coherent–perhaps as a orthogonally complex double helix going to oppositely placed detectors.  They oscillate their states, back and forth, until one detector captures and absorbs the momentarily real portion of the double helix, instantaneously leaving the orthogonal (imaginary at that moment) helix intact for discovery by the other detector at a later time.

This work provides a novel set of tools for looking at various quantum particle interactions.  I’m going to discuss some of what I’ve discovered on this website.  I am trying to be clear what is provable (stuff in that paper) or science fiction (these posts, for the most part, are guesses how things work and aren’t really provable at this point).  I will try to make a good case for my science fiction, that is, why I find my ideas attractive possibilities.

One example is the famous two-slit experiment.   When a single particle hits a barrier with two openings in it, it interferes with itself and only will land at certain target locations on the other side of the barrier.  Paradoxically, if you close one of the openings, now the particle will land on any target location.  I have considered the question: why does the second opening cause an alteration to the particle’s path?

The second Bohm interpretation (the leading contender of valid quantum interpretations) suggests that the particle is preordained to go through one or the other slit, but is guided to an interference controlled destination by the particle’s extended wave property going through two slits.  In this Bohm interpretation, when determining the time/space evolution of the particle wave function, a complex exponential (representing the wave from the second opening) is added to the particle wave function to mathematically guide the particle to the interference pattern target.  Two spherical waves will combine to produce various interference patterns–see the figure:

interference_pattern

The big problem with this interpretation is that work is done to move a particle.  If the particle was ordained to go through one opening to a target that is blocked when the second opening is opened, but instead goes to a nearby interference defined location, the Bohm interpretation says that the waves going through the second slit is somehow expending energy via some force being applied to the particle.   There is no evidence for such a force in nature.

There are no forces needed when using the group wave interpretation approach described in my paper.   The particle is merely defined by where the wave components sum to produce a localized group wave delta function or similar construct.  Interfering waves simply change the possible places where the “particle” will appear, and in fact the concept of particle region is set by how a detector absorbs the group wave.  In the region of the barrier, the concept of a particle becomes very ambiguous, but no waves are absorbed by the barrier .  Instead, they all pass through the openings, so a Fourier composition must reform the particle somewhere after the barrier that will eventually hit the target detector region.  No funny or weird alterations to the wave function are needed.

There are many more ideas like this that follow from assuming a group wave interpretation–one of the most important being that group wave particles will appear to be moving at constant speed regardless of the observer’s frame of reference–a foundation for special relativity.  Do you agree why the group wave concept is a cleaner approach than the Bohm interpretation?  I don’t think this is science fiction, but I couldn’t get any journal editors to see things the way I am….  😦

Agemoz

PS:  I use wave and wave functions interchangeably in this post–the concepts shown here are valid for both physical waves and probability distributions.

 

Tags:, , , ,
Posted in Physics | Leave a Comment »