Posts Tagged ‘particle zoo’

« Older Entries

4D Dual Spin Point Particle Quark-AntiQuark Annihilation

July 16, 2024

Edit: Looking at the LaGrangian (equation of motion) for the strong force, which has been developed and refined over decades, I kind of noped out on the dual-spin idea for quark/gluon interactions. I did get a good sense of what chromodynamic color is–it’s not a property of quarks or gluons, but a mathematical device that ensures which particles can interact with each other. One way to determine this is the fact that all color quarks interfere, and all color pair gluons interfere. I thought the coupling number tensor field adds a crazy degree of complexity that something simple like the 4D dual-spin point concept cannot begin to cover. It’s worth it to study the LaGrangian and SU(3) in more detail, but all this really does throw a monkey-wrench in the works for dual-spin point particles.

Edit #2: Added note that shows that the 4D dual-spin point particle concept not only shows a clean explanation (conversion of angular to linear momentum) for annihilation products of electron or quark particle/antiparticle collisions, but it also shows why those are the only direct products of the collision.

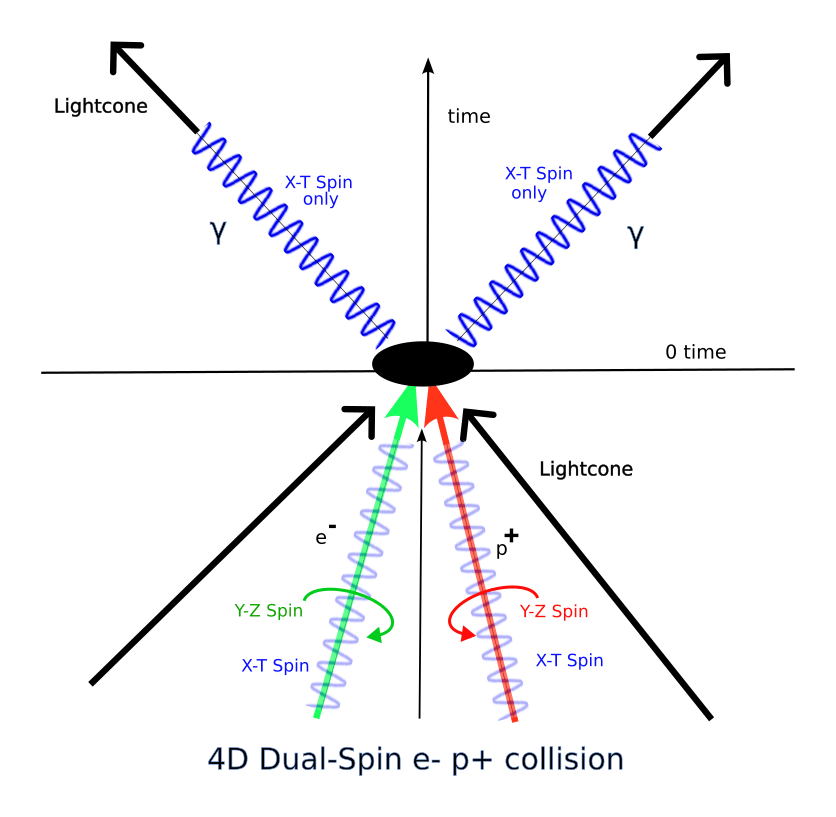
In the last post (https://agemozphysics.com/2024/05/12/spin-wave-functions-in-the-e-p-dual-spin-annihilation/), I showed how the analysis of 4D dual-spin point particle/anti-particle annihilation gives an elegant picture where annihilation is the process where one of the dual spins’ angular momentum components gets converted to the linear momentum of, for example, the resulting photons. This analysis then shows how to derive the quantized angular momentum /h (reduced Planck’s constant) of the source particles.

While this derivation was shown for the electron/positron annihilation case, there is nothing in the formula that limits to the electron/positron annihilation case. In fact, some beautiful results occur when you apply the same work to quarks. Unfortunately, there is a rather stinky fly in the ointment to this line of thinking.

Unlike lepton/antilepton annihilation, which can only annihilate to two photons, quarks can annihilate directly to either a pair of photons or a pair of gluons. Like photons, gluons have a transverse polarization angle, and like photons, they have no rest mass and thus move on the lightcone at the speed of light. Quarks have charge magnitude of either 1/3 or 2/3, and in the dual-spin point particle representation, this means that one of the two spins has a 1/3 ratio to the other.

The beautiful thing about this representation is that in quark annihilation, you can annihilate (convert to linear momentum) either the 1/3 spin, giving a photon pair result, or the 1 spin, giving a gluon pair result. Thus, the 4D dual spin point particle concept makes a case for covering all three annihilation cases, the lepton and both of two quark particle/antiparticle annihilation cases. Since the lepton case only involves 1/1 ratios, you never get a 1/3 spin result and hence never see annihilation into two gluons.

Edit: Note that a quark-antiquark annihilation has no other direct result products–all other collision products require intermediate particles within the collision neighborhood. That is a nice affirmation of the validity of the 4D dual-spin point particle concept–it not only shows an elegant and simple way to get the observed collision products for both electron and quark annihilation, but it also shows why those are the only results.

e-/p+ annihilation into two photons
q+/q- annihilation into two photons
q+/q- annihilation into two gluons

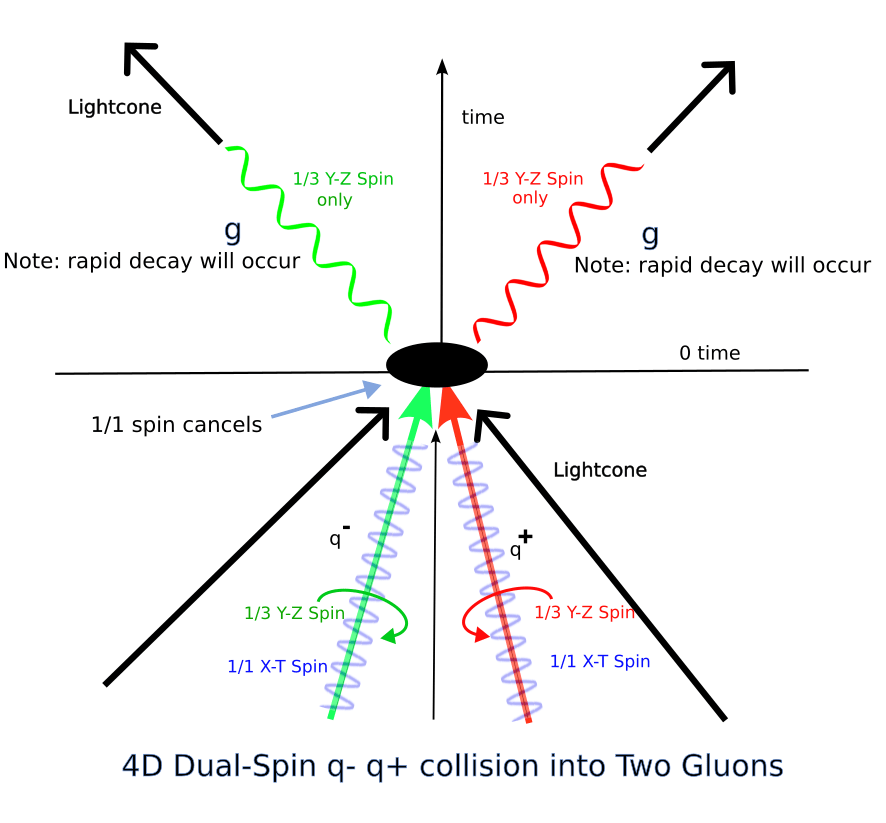
Unfortunately, the quark situation is actually not this simple–this does not show why we have chromodynamic color constraints on quark interactions.

In the Standard Model, we represent reality by two overlapping fields, the electromagnetic field covered by U(1), and the strong force field, covered by SU(3). The strong force field can be represented by a unitary constrained 8 dimensional real-valued adjoint (diagonally antisymmetric) matrix with eight orthogonal eigenvectors. The EM and strong force fields are clearly not completely independent, or else we could not have particles that stay in the same place on both fields when either electromagnetic or strong forces are applied. As a consequence, unification of the EM and strong force fields seems to imply there should be a single field representation, and with these annihilation analysis results, I had thought the 4D dual spin point particle concept would get us there.

However, I currently see no way that the 4 dimensional dual-spin point particle representation could be sufficient to constrain chromodynamic quark/gluon interaction characteristics. I’ve studied this for a while and think something has to be added to make the 4D dual-spin point particle concept fully work for quarks and gluons.

In summary, I do think that the four-dimensional dual-spin vector field is a good starting point for unifying the electromagnetic and strong forces–it certainly seems to provide an elegant view of several fermion/antifermion annihilations and pointing to how to get the quantized moments–but as is, it is not sufficient to cover quark/gluon chromodynamic color constraints.

Agemoz

Tags:, , , , ,
Posted in Physics | Leave a Comment »

Do Elementary Particle Conservation Laws Work for Dual-Spin Particles?

February 15, 2024

There are several conservation laws that define constraints on how elementary particles interact, and I’ve been looking at what they say about the R3+T dual-spin particle concept that I have studied (latest is at https://agemozphysics.com/2023/12/28/the-higgs-field-and-r3t-dual-spin-point-particles/). The idea here is to better determine whether dual-spin particles could work as a model for the Standard Model particle zoo.

If you have followed my study as shown in recent posts (e.g., https://agemozphysics.com/2023/12/17/properties-of-dual-spin-elementary-point-particles/), you know that I have found a number of properties of point particles that exist in our R3+T four dimensional spacetime. I believe it is indisputable that an elementary point particle in a four dimensional system can have two independent spins (for example, one spin in the X-Y plane, and another spin pointing within the Z-T plane). This fact, coupled with the fact that interactions in R3+T spacetime are confined to a 3D hypersurface slice that moves along the T dimension, results in quite a few very interesting properties that I list in previous posts. One very important property is the discovery that a single R3+T dual-spin particle can actually appear to us (as an observer within our hyperspace slice of R3+T) as two or three independent particles.

Up to this point, the work appears to be solid but does not prove if it is a basis for reality, that is, work as a structure for the interactions and particles defined by the standard model. One fairly quick way to make this determination is to see whether dual-spin particles conform to the standard model conservation laws. These laws constrain what particles can exist, and they also constrain decay paths. If dual-spin particles are a valid construct for reality, there should be no contradictions or impossible interactions.

The first conservation I looked at is the conservation of baryon number. This is the easiest one–since R3+T dual-spin particles are single particles that appear to us as multiple pseudo particles (see posts linked above), and quantization always limits the pseudo-particle count to either 2 or 3, baryon number will always be conserved in the dual-spin particle case. In fact, Noether’s principle states that this conservation law comes from the symmetry that actually implies a single particle (from some point of view within R3+T, not our hypersurface) for all quark combinations. I think that conservation of baryon number, combined with the requirement of relativistic invariance as applied to elementary point particles, directly points to the validity of the dual-spin structure. Looking good so far, at least to me.

Lepton number conservation also seems to work in the dual-spin system. There are quantized spin ratios of either two or three, and these cannot mix without dramatically changing the energy/mass of at least one of the pseudo particles–thus violating the conservation of energy of the system of interacting particles.

Fermion conservation is a somewhat general statement of momentum conservation, and I don’t see it affecting the argument of whether dual-spin particles would work or not.

I haven’t addressed muon number conservation because I don’t know what class of dual-spin ratios define muons. Similarly, isospin conservation requires a dual-spin ratio definition for the different pions and other particles. If I make progress by studying decay paths, I should see symmetries emerge here and how dual-spin structures fit within the isospin conservation constraint.

The crossing symmetry where an interaction can be transformed by taking the antiparticle of one of the components and placing it on the other side of the interaction equation should not affect the dual-spin validity.

Chirality needs more study. I don’t see anything that limits parity–dual-spin structures do not appear to favor one or the other reflection of an interaction. This would imply there is some other symmetry breaking activity taking place here, but does not rule out dual-spin as a valid representation of reality.

So, I am currently concluding that the conservation laws (other than the unknown case of muon and isospin conservation) do not lead to contradictions. In fact, baryon number conservation strongly points to the validity of the dual-spin structure as a basis for the particle zoo–in my opinion, for whatever that is worth…

Agemoz

Tags:, , , , ,
Posted in Physics | Comments Off on Do Elementary Particle Conservation Laws Work for Dual-Spin Particles?

R3+T Dual Spin Point Particle Appears as 3 Unique Particles in R3

November 21, 2023

We live in a 4 dimensional universe, three spatial dimensions and one time dimension. Point particles can have spin directions in all 4 dimensions, but because we perceive only an R3 slice of our R3+t existence (the “Activation Layer” hypersurface), there are surprising implications for point particle spins. One in particular is that a point particle can have two independent spins with integer ratios for spin cycle time. A 2:3 ratio of these spins in R3+T will cause the particle to appear to be three unique particles in R3!

Point particles that spin in 2 or 3 dimensions must rotate within a plane, but in 4 dimensions, there are two possible independent planes of rotation, for example in R1 + R2, and in the R3 + T directions. Thus, it is possible to have two simultaneous but independent spins in a 4 dimensional point particle, requiring no external angular forces to sustain the two independent angular momentums. In the last post, I created some images that demonstrate some of the possible rotation direction paths (these are directions, there is no physical displacement for a point particle spin):

A four dimensional dual spin particle with 1:1 rotation. Color represents the T direction
A dual spin particle with 1:3 rotation
A dual spin particle with 2:3 rotation

However, these pictures are misleading. It is very difficult for my mind to truly grasp what is happening when a four dimensional point particle spins in R3+T. These pictures shows the entire path in R3, with the part pointing in the fourth (T) direction represented by color, but in fact a 4 dimensional dual spin point rotation direction will actually appear and disappear from the R3 activation layer that we live in. Here is what the 2:3 case actually looks like:

Yes, you see what I see–in R3, a single 2/3 ratio dual spin particle looks like 3 stable, but unique spin directions over a time interval! The whole path is shown as a light color, but the locations where the spin direction (again, remember, these are spin directions, not displacements from a center point) lies in or close to R3 are shown in red. The path that lies in R3 show three separate components over time. The 1/3 ratio dual spin particle similarly show two different directions, but the 1:1 ratio case only shows 1.

I shamelessly speculate this is why we experimentally observe the appearance of three bound quarks in a proton and two bound quarks in a kaon, yet never observe isolated quarks. Dual spin particles rotating in the four dimensions of R3 and T provide a possible path to modeling the internal behavior of bound quarks. This is only the beginning–there are many possible rotation ratios that I think enables the entire particle zoo (both fermions and hadrons), and things like the 1/3 and 2/3 charge values emerge from this model.

UPDATE: The three “pseudo particles” that lie in the R3 plane are not all identical. I have previously hypothesized (see https://wordpress.com/post/agemozphysics.com/1722) that the second of two spin rates of an R3+T point particle (that does not include the T dimension) has to be responsible for both charge value and mass. Indeed, one of the three pseudo particles has double the angular momentum as the other two. Protons consist of two up quarks and one down quark with double the mass and half the charge, so the analysis of the dual-spin point particles continues to support the idea that the dual spins of R3+T point particles are responsible for the quark behavior of real-world hadrons.

Amazing stuff comes from thinking about point particles with dual spin in R3+T, I hope you think so too!

Agemoz

Tags:, , , , , , ,
Posted in Physics | Leave a Comment »

Geometry Model

January 13, 2022

If you are a scientist, be aware this is amateur work and there is nothing for you here. I use this site to help me keep track of my own thinking, which tries to adhere to known science but explores some “out-of-box” thinking to help synthesize my own world view of how I think things might work to explain subatomic particle existence. If physics is your profession, skip this, it’s not worth your time here.

There are previous posts from before the pandemic, there’s a lot of ideas there most of which I think are wrong. However, I’ve done a lot of thinking and some research since then, and am going to list here some that I think hold up to scrutiny. These foundational elements still seem to hold up and will form the basis for further work.

a: I am starting with the assumption that there is an underlying geometric basis for particles such as photons, electrons, and quark composites. This doesn’t necessarily hold true but for the purposes of my study I am assuming this.

b: Any group wave construction moving at some fixed speed in an observer’s frame of reference will classically doppler shift in such a way that an observer in some other frame of reference moving at some relative velocity will see the same group wave velocity. I wrote a paper on this that proves this, you can easily derive it yourself–take the Fourier transform of the group wave of a delta function deconstruction, then classically doppler shift these components before returning the group wave to the time domain. You will find that the velocity seen by the original observer is the same as that seen by the moving observer. Additional derivations show that any geometrical model of a particle that obeys special relativity must be composed entirely of waves, any non-wave components will not move at the same relative speed as the group wave and the particle will dissociate. Therefore, I am assuming that all elementary particles are formed entirely of some form of waves.

c: E=hv for all elementary particles describes a translation from a single unbreakable quantum of energy to a specific frequency. Therefore, at this frequency, only integer multiples of this energy are possible, and the only geometrical way to construct such quantization is by unitary vector rotations to and from a background state. I assume that elementary particles such as photons, electrons, and quarks consist of a single rotation in this background unitary vector rotation field.

d: I assume this background state cannot lie in R3, an additional imaginary dimension is required. If the background state were in R3, we would not see consistent particle behavior independent of the observer’s frame of reference (in particular, his rotation), and a cosmic background radiation would then become detectable that was dependent on the observer’s relative rotation. We do not see this, so therefore, I assume that elementary particles must consist of a vector wave rotation from and to the I part of an R3 + I vector field.

e: We already know from the standard model that every elementary particle emits a field of waves in the form of quantized virtual particles. Interference of these waves, for example in a two slit experiment, creates probability amplitudes for how the particle moves. However, these waves by themselves cannot define an elementary particle location. There must be a way to define the particle’s existence (within the constraints of the uncertainty principle) without introducing a non-wave entity (see assumption b above). I see that the only way to meet assumptions b and c is if the particle emits waves polarized in some direction v normal to the background state I, but the particle itself is defined by a complete integer twist normal to this set of polarized waves. Since this is essentially the second Bohm pilot wave model which is considered a leading model for quantum interference and entanglement, I am going to assume that this is the right construct for elementary particles.

f: Twists are not possible within a continuous field without introducing potential discontinuities, but are possible in a granular (quantized) field. I am assuming that the vector field allows this quantization and thus twists without causing energy discontinuities.

f: Photons travel linearly and have no rest mass, so I am going to assume that all of their energy is contained in the angular momentum of this wave twist normal to the I background state and the direction of travel. This defines the photon’s polarization.

g: All particles with mass are confined to a physical neighborhood, and because of the previous assumptions must consist of one or more wave twists as described in assumption e. A closed loop system of twists must move at the same speed c (otherwise the sum of their confined masses would vary).

h: At sufficiently high temperatures (more specifically, within a sea of high-energy photons since there are no known vibrational modes for electrons), electrons are known to dissociate into at least two photons, never a single one (because of momentum conservation). However, at rest, such dissociation will cause two photons of half the energy of the electron, and thus twice the wavelength of the electron energy wave. I am assuming that it is not possible to generate waves with this wavelength (unlike atomic emission, there are no vibrational states of the free electron that could generate longer wavelength photons). Therefore, I assume that electrons have to consist of two twists with doubled wavelength and hence half energy. I’m well aware that this contradicts the known point-particle behavior of the electron and currently am proposing that this two twist solution is completely inelastic and cannot exhibit any vibrational states.

i: If quantum interference defines the allowable probabilistic positions of these twists, and if these twists must always move at speed c (else their momentum would spontaneously change), there are only two possible stable constructions of twists. The first constraint forces the particle to lie in the region that is either 1/2 wave (for oppositely charged twists) or full wave (for identically charged twists), and the second constraint means that all twists in the system are moving in the same direction. I see only two solutions, both lying on a circle: the dipole, and a tripole. The dipole is obvious, but to enforce the tripole solution, there must be a pair of + twists separated by a full wavelength and a single – twist separated from the other two by a half wavelength that is a multiple of the full wavelength for the + twists. No other solutions in R3 are possible, although frequency multiples of these two solutions are possible. Note, this is not an EM field solution–no central force field can yield solitons on its own.

This ends the list of assumptions that I believe are sufficiently logical that I will base my model on them. What follows are attempts to find further constructions that will hold up.

I’m going to stop now and continue to add to this post in a bit.

Tags:, , , ,
Posted in Physics | Leave a Comment »

Virtual Photons

February 22, 2021

I did some research to understand the apparent difference between real and virtual photons. This has to be understood since radiation pressure and charge repulsion are models of each, respectively, and are fundamentally different from each other. Radiation pressure is quantized by E=hv and charge repulsion is not–a great example of the particle vs. wave dichotomy. My effort to find a basis for the particle zoo entities has to model this correctly. I have been trying to force-fit the unitary twist vector field into a particle zoo model, but ran into the issue of how to model charge and radiation pressure, or more precisely, the particle vs. wave behavior in real or virtual particles.

I had suspected that I was running into a definition problem: the difference has to do with the mistake of trying to describe real and virtual particles classically. At this tiny scale, defining a point can only be done with probability distributions–a more concrete definition doesn’t work because the actual entity doesn’t exist that way. QFT has various means of computing expected interactions in spite of that, but those of us insisting on a more detailed underlying structure are going to find ourselves without an infrastructure to derive results (and rolled eyes from the researches who understand this). I think I get the picture. The two types of interaction are different, but attempting to model the difference must take into account that geometric definitions such as the unitary twist vector field can’t model the entities very well if at all–the best we can do is the diffuse equations of probability distributions. I got hung up on trying to explain charge and virtual photons and the apparent point size of electrons via the unitary twist vector field, but now I see I really can’t do that.

Unfortunately, probability distributions have yet to show us why we have the particle masses and charge forces of reality. It will require a different approach than what I am doing to get there, though–a unitary rotation vector field might be a starting point, but I’m going to have to rethink the model. The only two clues I have found, other than what we already know from the Standard Model and quantum field theory, is that everything must consist of some type of wave (see this paper):

group_wave_constant_speed-1Download

and the quantization implied from E=hv (see this post):

agemoz.wordpress.com/2021/01/23/unifying-the-em-interactions/

It’s back to square one. I suppose the one good thing is now I know a little more than I did before…

Agemoz

Tags:, , , ,
Posted in Physics | Leave a Comment »

Linear Momentum Doesn’t Exist

August 19, 2020

That should be a controversial title and garner an immediate rejection from every physicist (I have lots of practice with that). However, it appears to be true as a model for our real world! Let me see if I can explain why I think this way.

I have been working on a simulator which models reality using a unitary vector rotation field with instantaneous quantum interference waves (not an EM field, a failed approach tried by many researchers in the past and even recently–reference DeBroglie, Compton, etc). Because this field has a background state, rotations are quantized, and these rotations generate waves mathematically identical to quantum interference components. By default, rotations propagate in R3 on a linear path and are modelled as photons, but two or more rotations can generate interference patterns that can form closed loops. These closed loops are modelled to be stable or unstable elementary particles. For more information on the details of these conclusions, you can reference previous posts on this website.

Two of the most important derivations from this work are the emergence of the constant speed of light from any wave based model of reality (see this paper: group_wave_constant_speed) , and the prediction for negative momentum carrying photons labelled antiphotons, which have yet to be discovered. Linearly propagating field rotations acting as photons (or antiphotons) carry momentum at speed c from source to destination, but being intrinsically massless, do not have any momentum of their own.

It is well known that photons emerge from atoms when bound electrons change state, that is, fall to a lower energy state. Alternatively, the atom can capture an incoming photon by raising the energy level of a bound electron. In the unitary rotation vector field theory, the electron emits a photon as a full field rotation with a specific angular momentum. At first glance, I concluded that the linear momentum of the electron gets converted to angular momentum to a linearly propagating rotation–a photon. When the photon is absorbed, the photon’s angular momentum gets converted to linear momentum in the target particle.

However, I ran into problems trying to incorporate this exchange in my simulation. Essentially, a photon interacting with a target electron (linear momentum exchange) or vice versa, was getting too much energy and not matching reality. I finally figured out what was wrong–the concept of linear momentum gets in the way of reality. There can be no such thing as linear momentum! It is an illusion caused by a particle that consists of closed loop field rotations, that is, it has angular momentum confined inside a finite region.

What actually happens when a particle is observed to have linear momentum is that the particle rotations are waves, and increasing the relative velocity of the particle does not add linear momentum. Instead, it causes the particle component composite waves to Doppler shift (note that in all cases in this post, I refer to classical Doppler shifting, not relativistic). When this Doppler shifted wave strikes some other object, the object receives an energy proportionate to the Doppler shifting, which is directly proportionate to the relative velocity of the particle. The Doppler shifting of the angular momentum of the particle is sufficient to explain the momentum change of the target particle, so the standard physics principle of linear momentum cannot actually exist.

The fundamental discovery here is this: The transfer of momentum from photon to electron or vice versa is entirely a transfer of angular momentum that can get Doppler shifted into higher or lower frequencies and hence higher or lower levels of angular momentum (and hence kinetic energy). Our reality, at least in this model of the universe, does not provide for the existence of linear momentum of objects!

Agemoz

Tags:, , , ,
Posted in Physics | Leave a Comment »

Resolving the Rotation Field Contradiction

February 27, 2020

A while ago, I discovered a showstopper–a contradiction between two parts of the theory I’ve been working on that proposes an underlying unitary rotation field for the particle zoo.  The theory is based, in part, on two discoveries:  that any Fourier construction of particles (a sum of waves that results in a group wave delta function) will appear to move at constant speed regardless of observer frame of reference, thus providing a basis for special relativity, and secondly, that quantized energy states can emerge from an R3+I unitary rotation field.  Lots of work has resulted from this basic model of existence, including the quantized formation of stable solitons.

However, the showstopper problem needed to be resolved, and I think I have done so, although I’ve not proven it yet.  The problem is this:  how can a sum of waves exist in a unitary single valued vector field?  There is no magnitude component in such a field, so the only way to “sum” a Fourier composition of waves is to sum the rotations at any given point.  This doesn’t really work when you try to classically doppler shift the resulting field, there’s no wave components present in the resulting field and the special relativity behavior can’t emerge.  I’ve looked at abandoning the doppler shift approach, but there are only a few other ways that special relativity could emerge and so far they all seem unworkable as an underlying field for particles.

Coming back to the original premise, I can resolve the paradox if doppler shifting can occur on a single wave cycle (rather than requiring a sum of waves).  I believe that this should be true for this reason–when generating a Fourier sum of a delta function, normally waves of infinite span are used.  However, in the limiting case, all parts of the sum cancel out except in the region of the delta function, so the constant speed derivation is just as valid if you only use the sum of waves in the immediate region of the delta function.  A single cycle of oscillation will still doppler shift, and the apparent constant velocity of the resulting delta function is valid whether the infinite waves are summed or the region bounded (single cycle) waves are summed.  If there is only a single cycle wave present, its shape and velocity are still defined by the math of the original theorem with a different set of limits (described in this paper: group_wave_constant_speed) and now the contradiction is resolved.

There’s more work to do, I think it would be pretty easy to blow holes in this framework as it is.  Nevertheless, it’s the first time I’ve been able to work out a promising answer to the showstopper contradiction.

Agemoz

 

Tags:, , , ,
Posted in Physics | Leave a Comment »

Rotation Field Momentum Transfer Induces Curvature

January 15, 2020

I am digging deep into the details of how an R3+I unitary vector field behaves.  I study this field because I’m hypothesizing that it is a good candidate for an underlying field that will produce the particle zoo of reality.  I’m not trying to figure out gravity or dark matter or any of that–I just want to find a workable underlying structure that could explain why there are stable and unstable particles, and why quantum creation operators evolve particle/antiparticle pairs.   If you take a look at some of my recent prior posts, you’ll see the thinking I used to come up with this field concept.

I really like this study, because it avoids the handwaving problem of trying to prove that some new idea represents actual reality.  Every amateur (and I’m sure most real-life physicists) have their pet idea of how things work, and the central problem in promoting that idea is not discovering new science, but rather the socio-political problem of convincing others, and in particular, professional researchers, that your idea is right.  That is a really hard problem that doesn’t involve actual science research.  I have attempted to publish papers in the past and have discovered that that activity is an exercise in futility.  What I love about my study of the R3+I unitary rotation field is that I leave that all behind–I’m just exploring how this field behaves, all the while keeping an eye out for something that might invalidate the field as a candidate for reality.

And to this end, I have discovered some great properties of this field.  The field so far shows the right degrees of freedom to produce linear and closed loop particles, shows why quantization occurs (the lowest energy state of the field is the +I rotation direction, confining twists to integer multiples of complete cycles) and clearly shows how the two types must interact.  Since (see previous posts) the field is blocking, a linearly propagating twist rotation through +I will propagate until it encounters a closed loop twist in this field.  Non-unitary fields such as an EM field permit varying vector magnitudes, including regions with zero magnitude.  In that type of field, there is no possible way that a linearly propagating twist can intercept and be absorbed by a closed loop through the center (think photon striking an electron).  But a unitary twist field, as shown in previous posts, has a very specific stable configuration of rotations that must exist in the center of the loop.  When a linearly propagating twist tries to collide with the closed loop, it cannot pass through (remember that unitary rotations cannot linearly combine, there is no magnitude other than 1).  It will pass its momentum components to the rotations in the loop, but cannot dissolve the loop unless the momentum of the linear particle approaches the momentum of the loop components and breaks the loop.  I know this sounds like handwaving, but I think if you do your own analysis of this field you will find this to be true.

Now on to the new findings:  as I dug deeper into the specifics of this interaction, I had to define exactly how rotation momentum would propagate through the rotation field, and in so doing discovered a very important principle, shown in the figure.  I described how momentum translates in spacetime with a single rule as follows–a delta rotation in R3+I propagates in the direction of rotation.  Quantization says that there must also be a background state restoration force (note that the momentum itself is not unitary, it can be zero or even infinite, and everything in between.  It’s only the vector magnitude that has to be unitary in the R3+I unitary vector field).  When looking at the geometry of this, I discovered something very important about the unitary rotation field R3+I–geometrically, if conservation of momentum is to hold, in certain circumstances, the momentum path must curve.

curved_momentum

Normally, if a quantized rotation twist propagates through the +I background rotation state, there is no reason why the momentum propagation rule wouldn’t ensure a straight line path.  However, suppose the twist passes through a region where the field is not at +I (the low energy state).  If this region is pointing orthogonal to the twist path, the resulting sum of the propagated twist rotation direction and the existing field direction would be linear and momentum magnitude and direction would be conserved.  But you cannot sum vector directions in this field–it is unitary, only rotations are allowed.  The only way the incoming momentum magnitude could be conserved is if the rotation follows a curved path (see illustration).

What this means is that in most circumstances, linear twists will propagate in a straight line since the default state for the path will be at the +I rotation direction.  But if it passes through a field region where there is an angle offset from +I (for example, in the neighborhood of a closed loop particle), it will curve in the plane of the angle offset and the direction of travel.  Two adjacent twists will curve antiparallel to each other and produce a sustained closed loop path, thus forming a field soliton.

In earlier posts, I hypothesized that quantum interference in an R3+I system would redirect a particle’s linear path and form a soliton–we know that to be true from experiments like the two-slit experiment, but I didn’t know why the curvature  would happen.  I was on the right path with quantum interference, but by breaking down how rotations must propagate, now I know geometrically that if we assume a unitary rotation vector field, then closed loop particles must occur.  Even better–the effect is contravariant.  That is, higher twist momentums lead to smaller closed loops.  In Newtonian physics’ descriptions of orbiting particles, the larger the momentum, the larger the resulting orbit.  The effect on path is covariant.  But you should be able to see (reference the figure) that in the R3+I unitary rotation vector space, the larger the momentum, the greater the curvature must be to conserve momentum magnitude, and the smaller the resulting path must be.  This field clearly provides the means for the contravariant relation between particle energy and particle wavelength–something no other theory that I know of has been able to explain.

Agemoz

 

Tags:, , , , ,
Posted in Physics | Leave a Comment »

Summary of Findings So Far

February 5, 2018

I took the time to update the sidebar describing a summary of the unitary twist field theory I’ve been working on.  I also paid to have those horrid ads removed from my site–seems like they have multiplied at an obnoxious rate on WordPress lately.

One problem with blogs describing research is the linear sequence of posts makes it really hard to unravel the whole picture of what I am doing, so I created this summary (scroll down the right-hand entries past the “About Me” to the Unitary Twist Field Theory) .  Obviously it leaves out a huge amount, but should give you a big picture view of this thing and my justification for pursuing it in one easy-to-get place.

The latest:  I discovered that the effort to work out the quark interactions in the theory yielded a pretty exact correlation to the observed masses of the electron, up quark and down quark.  In this theory, quarks and the strong force mediated by gluons is modeled by twist loops that have one or more linked twist loops going through the center.  This twist loop link could be called a pole, and while the twist rotation path is orthogonal to the plane of the twist loop, the twist rotation is parallel and thus will affect the crossproduct momentum that defines the loop curvature.  Electrons are a single loop with no poles, and thus cannot link with up or down quarks.  Up quarks are posited to have one pole, and down quarks have two.  A proton, for example, links two one-pole up quarks to a single two-pole down quark.

The twist loop for an up quark has one pole, a twist loop path going through the center of it.  This pole acts with the effect of a central force relation similar (but definitely is not identical to an electromagnetic force) to a charged particle rotating around a fixed charge source–think an atom nucleus with one electron orbiting around it.  The resulting normal acceleration results from effectively half the radius of the electron loop model, and thus has four times the rotation frequency and thus 4 times the mass of an electron.  The down quark, with two poles, doubles the acceleration yet again, thus giving 8 times the mass of an electron.

It will be no surprise to any of you that this correlates to the known rest masses of the electron, up quark, and down quark:  .511MeV, 2.3MeV, and 4.8MeV.

I can hear you screaming to the rafters–enough with the crackpot numerology!  All right, I hear you–but I liked seeing this correlation anyway, no matter what you all think!

Agemoz

Tags:, , , , , , , , , ,
Posted in Physics | Leave a Comment »

Unitary Twist Field Model for the Weak Force

January 31, 2018

The Unitary Twist Field theory posits that the particle zoo and corresponding exchange particles could form from a rotation (unitary magnitude) vector field.  I have put together a simulation of this field and appear to have confirmed it can form stable particles of various sorts, including a qualitative model using linked closed loops for quarks and the strong force.  Now I see a possible mechanism for the weak force in this theory.

The sim work clearly shows that if two closed loops such as rings are pulled apart to the point where the twists of each ring approach each other, there are dramatic effects on the rings that will separate or destroy both rings.  I was hoping to have the sim show that such linked rings will try to avoid (ie, push away from each other) what might be called a momentum collision as the twists approach each other, but right now I am running into a problem with the sim code.  I call this problem “momentum splitting”, and it results from the lattice computation of momentum progression in the sim.  Since momentum almost never transfers exactly into an adjacent sim cell, either the conserved momentum must be split between two or more cells, or all of it must be sent to one of the adjacent cells, with the result that some of the momentum location information is lost or rapidly spreads throughout the array.  In both cases, the sim results go badly awry from actual expected results.  I am working on a solution that enforces conservation of momentum by using the second option, but keeping a separate array of momentum parameters such as exact location in each cell.

So–a roadblock to getting good sim results, but often working out details of the sim yield insights to the actual model.  One thing I noticed about the twist field model (not the sim of the model) is that there is a very small probability that two twist rings will collide in such a way that the twist rotation angle happens to be identical.  If this happens, there is sort of a quantum tunneling effect where the two rings can separate if a random jiggling of the rings hits this coinciding angle rotation.  At that point, the rings would have to disintegrate or form other loop combinations (my hypothesis) because the ring energies are not correct for stability on their own.  I originally thought this was a fatal flaw in the linked ring idea for quarks–but then I realized that the vast majority of quark combinations are not stable, they decay via the weak force.  Up to now, I couldn’t see any way to get the Unitary Twist Field to model the random effect of the weak force, but this is a great solution, I think!  The random thermal motion of our existence would be constantly pulling and pushing the linked rings in a very chaotic way, and every once in a while the ring rotations at the point of collision would line up and cause a dramatic breakup of the linked structure.  Just about all of the linked quark combinations experience decay in varying amounts of time, and this model of the unitary twist field provides a means for this to happen.

So–how do I explain the stability of the proton?  And why does the nearby presence of a proton make a neutron stable?  I suspect that in the case of the proton, even if this ring tunneling happens, the decay must result in something else that the separated rings can decay into (to conserve momentum, among other things).  If there isn’t something to decay into, the proton component tunneling of quark rings won’t occur even if the rotations at the collision point line up correctly.

The neutron case is a lot more interesting, I don’t have an answer but I continue to think about it.  My leading hypothesis is that the proton-neutron combination is actually some unique combination of linked rings that can decay into separate particles (free neutron and proton).

Agemoz

Tags:, , , , ,
Posted in Physics | Leave a Comment »

« Older Entries