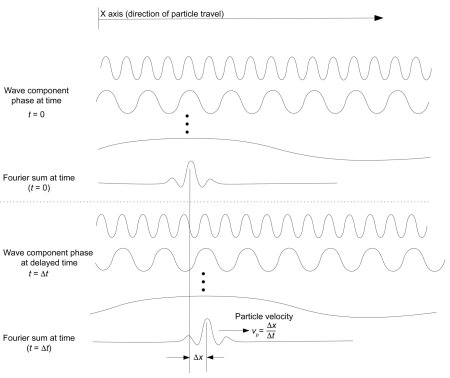
In the previous post, I showed a proven theorem where classical Newtonian particles composed of instantaneous phase waves must observe special relativity. If we assume the converse is true, it becomes worthwhile to deconstruct subatomic particles, which obey the principles of special relativity, as some construction of instantaneous phase waves.
Fortunately, quantum experiments such as the two-slit experiment and the Aspect experiment already confirms this principle: there is good evidence there are instantaneous phase waves in particles because of the experimentally observed noncausal decoherence of entangled particles. In addition, the two-slit experiment also shows that this interference is noncausal–you can cover one of the slits in the time it takes for a particle to travel through slits to a target detector, and instantaneously alter the possible particle detection sites. Assuming that particles are formed by nothing other than waves has significant justification, both due to experimental observation and because such particles must obey special relativity according to the theorem described in my paper (see previous posts).
So–if we assume that particles form only from composite collections of waves, can we infer from the experimentally observed quantum interference patterns what the subatomic particles must look like mathematically?
There’s a lot of reasons we might be tempted to describe electrons with a Compton radius size, but any serious physicist won’t believe such claims, here’s why. Subatomic particles are most often measured and examined in collision experiments. The actual collision can’t be observed in most cases, but the resulting particle trajectories and masses can be, and allows us to determine things like size, internal composition, and angular momentum of the colliding particles. One nice way to determine internal composition is to measure elasticity. If you hit a billiard cue ball against another billiard ball, it might bounce right back at you, whereas if you throw a water balloon at another water balloon, the whole mess of water and balloon fragments will head more or less in the direction of your throw. In other words, we can gain a lot of information about the inelasticity of a particle by the angular distribution of the post-collision particles. All experiments show that electrons are perfectly elastic and are measurably infinitely tiny. Hard as a billiard ball and too small to measure any diameter.
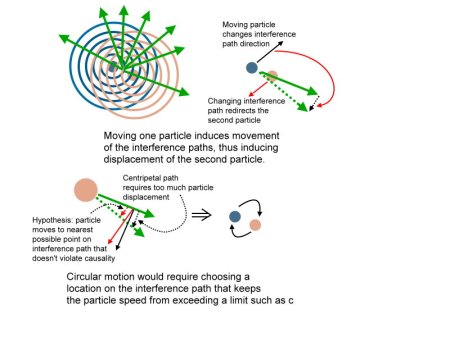
Here’s the problem–if you test the hypothesis that particles can form group wave constructs affected by quantum interference effects, we can draw conclusions based on knowing that the particles must be composed of instantaneous phase waves. These waves don’t have to lie in a plane–for example, waves that lie on a twisting plane obey the same Fourier composition rules as planar waves. I hypothesized in the previous several posts that waves form a couple of opposing delta functions that follow the peaks of the self-generated quantum interference wave pattern. We already know from the two-slit experiment that quantum interference will redirect a particle path onto the peaks of the quantum interference that results from passing the waves through two slits. It is thus very reasonable to assume that the right setup of quantum interference would create a circular loop, and I show that in the previous two posts.
However, this wont work if the two poles of our particle are infinitesimally spaced, that is if the particle has no significant size such as a Compton radius. The poles are too close to be able to fall into the quantum interference peak locations that guide them into a loop ring!

The only way–and it seems like a tenable proposition–is to say that the electron is not an infinitesimal point, but rather, a ring whose axial diameter is infinitely small. Now the collision cross-section is the same as the point particle and you should get the same experimentally observed angular distribution of post-collistion particles–provided that the ring does not collapse–that it is totally inelastic. I proposed this to an experienced particle physicist, but he said that’s not possible–there should be observable characteristics of a ring that are different than for a point particle. I tried to argue that there’s a better argument for a ring than a point, because a ring has a definite angular moment (electrons have an experimentally measurable angular moment) but a point as defined as such does not. I see a strong case for my proposition from the quantum interference soliton point of view, the angular moment, the Planck’s constant uncertainty relation (which says that something smaller than the Compton radius cannot meet the position-momentum Heisenberg uncertainty relation), and many others. As you can imagine, I didn’t get very far–the response was NO, subatomic particles are measurably infinitesimal points! And that’s all he would discuss.

Regardless–it appears clear to me that examining the experimentally observed quantum interference pattern of a particle should tell us new information about what forms the particle. Is quantum interference responsible for particle structure? If it is, the particle has to be a lot bigger than an infinitesimal point, yet have the collision signature of a point. The only answer I see is the ring hypothesis with an infinitesimal axial radius. Otherwise, I will have to conclude that quantum interference must be refuted as a candidate for forming solitons, and hence, subatomic particles, from waves.
Agemoz