I posted here for the first time in almost two years that I wrote a physics paper and posted the attachment (see previous post). After doing all the work on the paper and going through the publishing process I kind of decided that was enough of that. It’s exhausting work and I gained a new appreciation of the work PhD candidates go through. No, the paper didn’t get published after four tries, mostly “not in the scope of the journal”–but I did learn a lot about being thorough and detailed. I like to think I’m a little less of a crackpot for going through the process.
I decided to go back to posting about my research work here, which is a lot more fun and allowed me more time for research, reading Arxiv articles, and running sims. The cool thing about the research described in my paper was the creation of new computational tools for simulating particle interactions using a new quantum interpretation–so I have lots of ideas where to go from here.
I will try not to post too often, and try to limit speculation–in other words, build your trust that this is a site worth going to and not waste your time. Comments are always welcome although I can be pretty slow in responding.
Since everyone loves reading a paper (not), let me summarize what I did in that paper. I hypothesized that a new quantum interpretation is needed for extending the Dirac equation to predict quantum interference effects. This interpretation is based on the group wave principle–that particles are formed when a Fourier composition of waves sum to an analytic function such as a delta function. Each wave component has instantaneous phase–that is, changing the phase of a wave component takes effect instantaneously across the wave (see the figure). Causal limits on the particle result from a limitation on the rate of change of any wave phase. The paper provides a mathematical proof that such a Fourier sum will always appear to be moving at a constant speed regardless of the frame-of-reference velocity of the observer, thus deriving a basic postulate of special relativity and validating the quantum interpretation over our current set of interpretations.
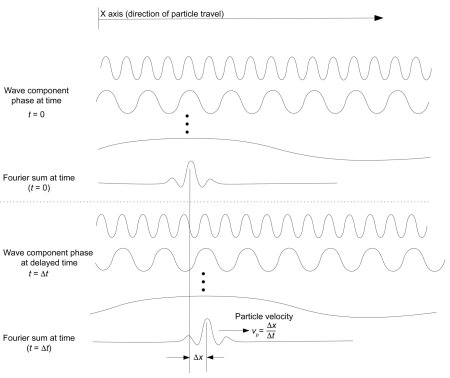
FIG. 2. Instantaneous change in phase across waves on x-axis for each value of time t
This interpretation leads to a bunch of derivations I want to explore. I describe a simple example in the paper for entangled particle decoherence. Another of my favorites is how the interpretation explains “particle or wave” in the dual slit experiment. Using this approach, it’s very easy to see that the group wave particle is intact until it nears the barrier with two slits. At that point the definition of where the particle is becomes very ambiguous–but math will show the particle group wave re-appears after it clears the barrier. I’ll show some sims once I get them completed with pictures (or tell you that I was unsuccessful. I’m probably still a crackpot, but I try to be an honest one!)
Agemoz