I last posted on my discovery that any classical group wave will obey the observed constant speed property, a prerequisite (one of the two assumed postulates) for special relativity. That is, if you throw a baseball, its speed will be some value v_p. If you are standing on a train moving in the same direction at speed v_e, an observer on the ground will see the baseball move at speed v_p + v_e. But, if you throw an object that is a linear sum of waves, such as a delta function group wave, it doesn’t matter what v_e (the relative speed of the thrower) is, the observer on the ground will always see it move at speed v_p.
The math and concept seemed bullet-proof, so I spent a couple of years writing a paper and trying to get it published. I stayed away from any speculation and just wrote a proof that says classical group waves must appear to move at some constant speed v_p regardless of an observer’s frame of reference velocity v_e. I made sure there was nothing in there that would make a reviewer immediately toss the paper. I worked on getting the format and grammar acceptable for scientific publishing, had several reviewers check it for errors and conceptual problems. They claimed it was good to go so then I submitted to several journals. No luck–a bunch of rejections later and I finally gave up. However, no editor wrote to disprove my math or the conceptual thinking, not sure they ever looked at that–it was always the paper doesn’t meet the quality standards of the journal or some such reason (if any). In spite of my best skeptical analysis, I cannot find fault with the derivation, and I still think there’s some science here, so I decided to forget the publishing effort and just continue seeing what I could discover on my own.
Here it is: group_wave_constant_speed
Unlike many of the ideas I post here, which are guesses how things work and are borderline science fiction, I thought this work was a small breakthrough, it says several important things. First, if this is true (represents reality), it shows why special relativity exists in our universe. All the research I have done shows that no one has determined why we assume the constant speed of light postulate holds and thus why we have special relativity behavior. Second, it shows that every particle and exchange particle must consist entirely of some kind of a wave summation, otherwise it would violate special relativity–thus giving an important clue how to mathematically define subatomic particles. And third, it shows that any quantum particle composed of waves must phase shift the waves at a causal rate–but there can be no time-dependent component to the phase-shift along the length of the wave. In other words, the entire wave component shifts non-causally, albeit at a causal rate. This is important because now the Aspect experiment makes sense–if entangled particles are emitted in opposite directions, the particles stay coherent–perhaps as a orthogonally complex double helix going to oppositely placed detectors. They oscillate their states, back and forth, until one detector captures and absorbs the momentarily real portion of the double helix, instantaneously leaving the orthogonal (imaginary at that moment) helix intact for discovery by the other detector at a later time.
This work provides a novel set of tools for looking at various quantum particle interactions. I’m going to discuss some of what I’ve discovered on this website. I am trying to be clear what is provable (stuff in that paper) or science fiction (these posts, for the most part, are guesses how things work and aren’t really provable at this point). I will try to make a good case for my science fiction, that is, why I find my ideas attractive possibilities.
One example is the famous two-slit experiment. When a single particle hits a barrier with two openings in it, it interferes with itself and only will land at certain target locations on the other side of the barrier. Paradoxically, if you close one of the openings, now the particle will land on any target location. I have considered the question: why does the second opening cause an alteration to the particle’s path?
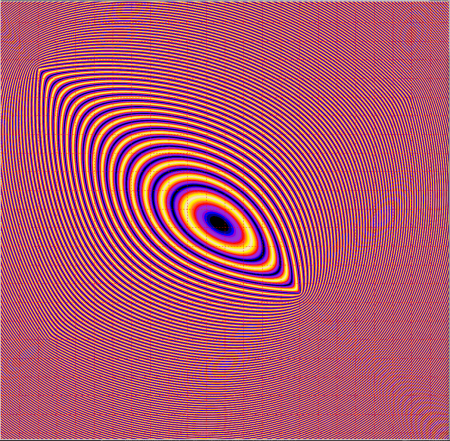
The second Bohm interpretation (the leading contender of valid quantum interpretations) suggests that the particle is preordained to go through one or the other slit, but is guided to an interference controlled destination by the particle’s extended wave property going through two slits. In this Bohm interpretation, when determining the time/space evolution of the particle wave function, a complex exponential (representing the wave from the second opening) is added to the particle wave function to mathematically guide the particle to the interference pattern target. Two spherical waves will combine to produce various interference patterns–see the figure:

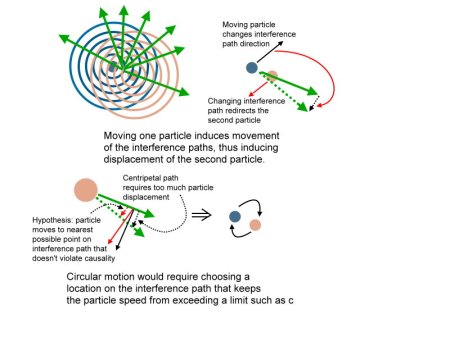
The big problem with this interpretation is that work is done to move a particle. If the particle was ordained to go through one opening to a target that is blocked when the second opening is opened, but instead goes to a nearby interference defined location, the Bohm interpretation says that the waves going through the second slit is somehow expending energy via some force being applied to the particle. There is no evidence for such a force in nature.
There are no forces needed when using the group wave interpretation approach described in my paper. The particle is merely defined by where the wave components sum to produce a localized group wave delta function or similar construct. Interfering waves simply change the possible places where the “particle” will appear, and in fact the concept of particle region is set by how a detector absorbs the group wave. In the region of the barrier, the concept of a particle becomes very ambiguous, but no waves are absorbed by the barrier . Instead, they all pass through the openings, so a Fourier composition must reform the particle somewhere after the barrier that will eventually hit the target detector region. No funny or weird alterations to the wave function are needed.
There are many more ideas like this that follow from assuming a group wave interpretation–one of the most important being that group wave particles will appear to be moving at constant speed regardless of the observer’s frame of reference–a foundation for special relativity. Do you agree why the group wave concept is a cleaner approach than the Bohm interpretation? I don’t think this is science fiction, but I couldn’t get any journal editors to see things the way I am…. 😦
Agemoz
PS: I use wave and wave functions interchangeably in this post–the concepts shown here are valid for both physical waves and probability distributions.