Posts Tagged ‘quantum’

« Older Entries
Newer Entries »

Noncausal Characteristics of Quantum Interference Solitons

July 6, 2019

In physics I fully understand the need to filter out the crackpots and their onslaught of verbiage, whether wrong, vague, incomplete, or meaningless.  Real science is built on a very large collection of proven concepts–if any component is wrong but makes it into the collection, trust in the system as a whole is damaged.  If you look at Arxiv.com, there’s some junk that somehow got in there, and that means you need some system of qualifying what you see so you can trust what you use in your own work.  To avoid this, new papers submitted to journals always require verification by qualified reviewers.

The problem I am having is that I tried very hard not to be a crackpot, I think i proved something important, wrote a paper that got good qualified pre-reviews, and submitted 5 times and got 5 rejections.  Nobody looked at the proof and said I did something wrong, and nobody showed me why my conclusion was wrong.  Two of the journals were probably not the right target for the paper (this), but the other three did not see value in what I did.  The trouble is–I still think the idea is important, and that the proof is valid (confirmed by the pre-reviews).

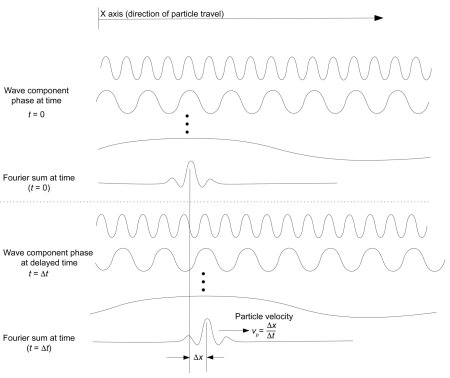
Basically, in the paper, I proved that if a classical Newtonian particle is formed by a Fourier composition of a specific class of waves, the particle must obey the principles of special relativity.  The class of waves is simple–a phase change across any wave component is noncausal, that is, instantaneous across the length of the wave, but the rate of change of that phase is causal, or limited to some maximum change per unit of time such as the speed of light.

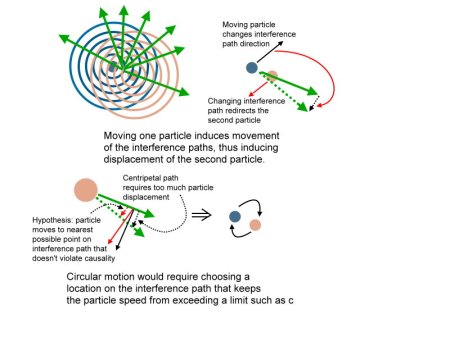
To me, this is incredibly important because it suggests the converse–if something obeys the principles of special relativity, it must *only* be composed of instantaneous phase waves.  I haven’t proven the converse–working on it–but if this is true, then this opens a big door into what causes the existence of subatomic particles.  A logical analysis of the two-slit experiment and the entangled particle decoherence behavior comes from the paper’s derivation (discussed in previous posts).  It also shows how a soliton (stable construct) could emerge due to quantum interference (see the last two posts).  And now, it shows specifically how the waves have to exist in the first place–very specifically showing what oscillations form the waves and where causality comes from.  From this, I see how the concepts of space and time might emerge out of something like the Big Bang.

You see, if a delta function of some sort is present in 3D space, and it is composed of these instantaneous phase waves, you *cannot* see the delta function do this:

single_spiral

The waves are instantaneous!  Here you see variations in space (and time, if you were to make a movie of the particle).  But that’s not possible with one delta function–it does not oscillate.  Oh, ok, no problem, handwave it and make it oscillate from a + to – peak and back again.  You *still* would not see this first figure–the wave phases are instantaneous, but this picture has variations in space and time.  Even if you put two of these delta functions near each other, one that is Pi/2 out of phase with the other, you would see something like this, where the two delta functions oscillate up and down out of phase with each other (this shows the Pi/4 halfway point):double_deltaThere are no waves here, because the sum of the delta functions can never produce anything but a plane, no matter how fast they oscillate in time.  I realized that now I think I know why electrons are not deBroglie circular waves with a Compton radius size–they have to be infinitely small.  The waves shown in the first figure have to result from a non-causal sum of a rotating and infinitesimally spaced, oscillating pair (or more) of delta functions.  Space and time for a particle emerge in a non-causal way from the orbiting pair of oscillating delta functions to produce the spiral waves shown in the first figure.  Only then could you see non-causal spiral waves emerge.  There’s other work I’ve done that shows that the delta functions must reflect some sort of twisting vector field in R3 + I  (NOT an EM field vector, those are photons).  Along the same lines, I’m sure you’ve seen the recent experimental observation of twist momentum found in photons.  Can you see why I see so much exciting work emerging from the simple theorem proof I describe in the paper?  Frustrating not to be able to publish it–I think I have something there, but can’t convince anybody else of it!  And until someone else sees the validity of what I’ve done, there’s no science here.

Auuggh!

Agemoz

 

Tags:, , , ,
Posted in Physics | Leave a Comment »

Quantum Interference Defines a Soliton: Part II, Computed Images

June 20, 2019

Here are actual computed results of how the interference pattern moves for a dual interference source.  In my previous post, I described how a moving interference pattern will alter the location displacement of the interference sources, which leads to the conclusion that quantum interference should enable stable solitons.  There, I showed a schematic representation of what should happen.  Here is visual computed proof that what I described actually happens:  The first picture shows no orthogonal displacement of the interference sources, so the interference paths are symmetric about the interference source X axis.  However, the following pictures demonstrate more and more successive orthogonal Y displacement, causing the interference peak paths to rotate in such a way as to displace the nearby interference source.  This assumes that the interference source will follow the rotating interference path–we know this is true due to experimental verification via the two-slit experiment as one example.  As a result, you should see that moving one interference source should cause the adjacent interference source to move in the opposite direction, causing the two sources to orbit like a binary star (see the previous post for details).

Notice the white line, this is the X axis reference direction to help assess the interference path rotation as y-axis displacement is added to one of the interference sources.  These examples show just one possible interference system–it shouldn’t be unreasonable that I conclude that all planar non-degenerate interference cases should behave the same way.  Things get really interesting when one of the sources is rotated into the Z axis, and when a third source is placed on the Z axis, and when the wavelength of one of the sources is doubled or multiplied by other factors such as 1/3 or 2/3.  More to come…

Agemoz

Edit:  My initial analysis (see previous post) showed that the two interfering sources would cause a rotating interference pattern if one were to move past the other in the direction orthogonal to the axis that both sources lie on.  I could show that there would be an induced motion to the second source if the first source were moved orthogonally, but did not know what would keep the second source from moving centripetally (moving away from the center).  Closer examination (see zoomed in picture) shows that there is a potential well in both the X and Y direction–the interference pattern itself is what constrains the radius of the orbiting path.  I do not need to invoke something like the speed of light to keep the orbital path confined to its radius.

sum_radials_00

sum_radials_10

sum_radials_20

 

sum_radials_30

Edit:  My initial analysis (see previous post) showed that the two interfering sources would cause a rotating interference pattern of rays if one were to move past the other in the direction orthogonal to the axis that both sources lie on.  I could show that there would be an induced motion to the second source if the first source were moved orthogonally, but did not know what would keep the second source from moving centripetally (moving away from the center).  I tried to bring in something, the speed of light, to confine the radius of the interference particle orbit, but soon felt like this was a flaw in my scheme for describing a soliton via interference (this is the same reason that various DeBroglie/Compton schemes using an EM field fail).  However, closer examination (see zoomed in picture) shows that the interference pattern is a potential well in both the X and Y direction–the interference pattern itself is what constrains the radius of the orbiting path.  The rays in the previous images are actually interference zeroes, not peaks–the particles will follow a path defined by the peaks.  I do not need to invoke a contrivance like the speed of light to keep the orbital path confined to its radius.

interference_well

Agemoz

Tags:, , ,
Posted in Physics | Leave a Comment »

Quantum Interference Defines a Soliton

June 18, 2019

In my last post, I described a quantum interpretation based on group waves with an instantaneous wave phase property, and showed how it derives a constant speed regardless of an observer’s frame of reference, setting the stage for special relativity.  I also showed how it would resolve the EPR (Einstein-Podolsky-Rosen) paradox for entangled particles in the Aspect experiment cleanly without adding some unknown force.  This is a flaw with the Bohm interpretation, among others, since it means that work is done and energy expended, causing a conservation of energy violation.  We do not need to believe in multiple parallel universes (Everett interpretation) or try unsuccessfully to create a logically consistent causality using the Copenhagen interpretation.

I then showed how a instantaneous phase group wave particle could self-interfere in the two-slit experiment to logically explain the target interference pattern distribution.  In this explanation, I show the very nature of the group wave will cause particle displacement due to the summation of interfering wave components.  No pilot wave guiding, with its implied force and consequent work and energy expended, is needed.

I suddenly realized that the group wave quantum interpretation provides a possible approach for creating a soliton–a particle could form in a system based on this quantum interpretation.

For over a century, theoretical researchers have guessed that the particle zoo (the list of subatomic particles that make up protons, atoms, exchange forces, and so on) could form from a continuous field (lattices, i.e., discrete fields, have been ruled out at this time both experimentally and theoretically).  DeBroglie was one of the earliest well known scientists that worked with this idea, but Compton and others also came up with proposals.  Early efforts assumed that solitons might form from an electromagnetic field via some selected arrangement of charge distribution, but EM fields and particles have the central force property F = c_0 q_1 q_2/(r^2), and by Maxwell’s field equations behave linearly, so basing particle existence on an EM field was disproved–particles would dissipate.  If there is a field underlying formation of particles, it cannot be electromagnetic, but rather an underlying “precursor” field from which EM fields could emerge.  Dirac’s work led the way to the modern quantum field theory, which further ruled out an EM field creating solitons–EM fields consist entirely of collections of real and virtual photons that travel in straight lines (ignoring space curvature from general relativity at quantum scales).

But instantaneous phase group wave theory can form solitons.  No matter what quantum interpretation you believe in, you have to face the fact that a single particle going through two slits is going to experience redirection when you open one of the slits.  The fact that this redirection happens means that at some scale, a particle will curve in on its path–it must follow the interference pattern.  I have found a variety of ways that a moving interference pattern will circulate or follow more complex loop variations.  For the same reason that the two-slit setup forms an interference patterned domain of existence for a particle, the appropriate pair (or more) of particles will self interfere to form stable loops.  Follow the interference and you will describe a variety of possible particle paths.

Does this reflect reality–dunno, but work is ongoing.  I’m coming up with a mathematical toolset that will describe various interference path constructions.  I will follow the yellow brick road and see where it leads…interference_path_soliton

Agemoz

Tags:, , , ,
Posted in Physics | Leave a Comment »

Why Does Quantum Interference Affect Particle Path?

June 11, 2019

I last posted on my discovery that any classical group wave will obey the observed constant speed property, a prerequisite (one of the two assumed postulates) for special relativity.  That is, if you throw a baseball, its speed will be some value v_p.  If you are standing on a train moving in the same direction at speed v_e, an observer on the ground will see the baseball move at speed v_p + v_e.  But, if you throw an object that is a linear sum of waves, such as a delta function group wave, it doesn’t matter what v_e (the relative speed of the thrower) is, the observer on the ground will always see it move at speed v_p.

The math and concept seemed bullet-proof, so I spent a couple of years writing a paper and trying to get it published.  I stayed away from any speculation and just wrote a proof that says classical group waves must appear to move at some constant speed v_p regardless of an observer’s frame of reference velocity v_e.  I made sure there was nothing in there that would make a reviewer immediately toss the paper.  I worked on getting the format and grammar acceptable for scientific publishing, had several reviewers check it for errors and conceptual problems.  They claimed it was good to go so then I submitted to several journals.  No luck–a bunch of rejections later and I finally gave up.  However, no editor wrote to disprove my math or the conceptual thinking, not sure they ever looked at that–it was always the paper doesn’t meet the quality standards of the journal or some such reason (if any).  In spite of my best skeptical analysis, I cannot find fault with the derivation, and I still think there’s some science here, so I decided to forget the publishing effort and just continue seeing what I could discover on my own.

Here it is: group_wave_constant_speed

Unlike many of the ideas I post here, which are guesses how things work and are borderline science fiction, I thought this work was a small breakthrough, it says several important things.  First, if this is true (represents reality), it shows why special relativity exists in our universe.  All the research I have done shows that no one has determined why we assume the constant speed of light postulate holds and thus why we have special relativity behavior.  Second, it shows that every particle and exchange particle must consist entirely of some kind of a wave summation, otherwise it would violate special relativity–thus giving an important clue how to mathematically define subatomic particles.  And third, it shows that any quantum particle composed of waves must phase shift the waves at a causal rate–but there can be no time-dependent component to the phase-shift along the length of the wave.  In other words, the entire wave component shifts non-causally, albeit at a causal rate.  This is important because now the Aspect experiment makes sense–if entangled particles are emitted in opposite directions, the particles stay coherent–perhaps as a orthogonally complex double helix going to oppositely placed detectors.  They oscillate their states, back and forth, until one detector captures and absorbs the momentarily real portion of the double helix, instantaneously leaving the orthogonal (imaginary at that moment) helix intact for discovery by the other detector at a later time.

This work provides a novel set of tools for looking at various quantum particle interactions.  I’m going to discuss some of what I’ve discovered on this website.  I am trying to be clear what is provable (stuff in that paper) or science fiction (these posts, for the most part, are guesses how things work and aren’t really provable at this point).  I will try to make a good case for my science fiction, that is, why I find my ideas attractive possibilities.

One example is the famous two-slit experiment.   When a single particle hits a barrier with two openings in it, it interferes with itself and only will land at certain target locations on the other side of the barrier.  Paradoxically, if you close one of the openings, now the particle will land on any target location.  I have considered the question: why does the second opening cause an alteration to the particle’s path?

The second Bohm interpretation (the leading contender of valid quantum interpretations) suggests that the particle is preordained to go through one or the other slit, but is guided to an interference controlled destination by the particle’s extended wave property going through two slits.  In this Bohm interpretation, when determining the time/space evolution of the particle wave function, a complex exponential (representing the wave from the second opening) is added to the particle wave function to mathematically guide the particle to the interference pattern target.  Two spherical waves will combine to produce various interference patterns–see the figure:

interference_pattern

The big problem with this interpretation is that work is done to move a particle.  If the particle was ordained to go through one opening to a target that is blocked when the second opening is opened, but instead goes to a nearby interference defined location, the Bohm interpretation says that the waves going through the second slit is somehow expending energy via some force being applied to the particle.   There is no evidence for such a force in nature.

There are no forces needed when using the group wave interpretation approach described in my paper.   The particle is merely defined by where the wave components sum to produce a localized group wave delta function or similar construct.  Interfering waves simply change the possible places where the “particle” will appear, and in fact the concept of particle region is set by how a detector absorbs the group wave.  In the region of the barrier, the concept of a particle becomes very ambiguous, but no waves are absorbed by the barrier .  Instead, they all pass through the openings, so a Fourier composition must reform the particle somewhere after the barrier that will eventually hit the target detector region.  No funny or weird alterations to the wave function are needed.

There are many more ideas like this that follow from assuming a group wave interpretation–one of the most important being that group wave particles will appear to be moving at constant speed regardless of the observer’s frame of reference–a foundation for special relativity.  Do you agree why the group wave concept is a cleaner approach than the Bohm interpretation?  I don’t think this is science fiction, but I couldn’t get any journal editors to see things the way I am….  😦

Agemoz

PS:  I use wave and wave functions interchangeably in this post–the concepts shown here are valid for both physical waves and probability distributions.

 

Tags:, , , ,
Posted in Physics | Leave a Comment »

Paper Synopsys–A new Quantum Interpretation

May 5, 2019

I posted here for the first time in almost two years that I wrote a physics paper and posted the attachment (see previous post).  After doing all the work on the paper and going through the publishing process I kind of decided that was enough of that.  It’s exhausting work and I gained a new appreciation of the work PhD candidates go through.  No, the paper didn’t get published after four tries, mostly “not in the scope of the journal”–but I did learn a lot about being thorough and detailed.  I like to think I’m a little less of a crackpot for going through the process.

I decided to go back to posting about my research work here, which is a lot more fun and allowed me more time for research, reading Arxiv articles, and running sims.  The cool thing about the research described in my paper was the creation of new computational tools for simulating particle interactions using a new quantum interpretation–so I have lots of ideas where to go from here.

I will try not to post too often, and try to limit speculation–in other words, build your trust that this is a site worth going to and not waste your time.  Comments are always welcome although I can be pretty slow in responding.

Since everyone loves reading a paper (not), let me summarize what I did in that paper.  I hypothesized that a new quantum interpretation is needed for extending the Dirac equation to predict quantum interference effects.  This interpretation is based on the group wave principle–that particles are formed when a Fourier composition of waves sum to an analytic function such as a delta function.  Each wave component has instantaneous phase–that is, changing the phase of a wave component takes effect instantaneously across the wave (see the figure).  Causal limits on the particle result from a limitation on the rate of change of any wave phase.  The paper provides a mathematical proof that such a Fourier sum will always appear to be moving at a constant speed regardless of the frame-of-reference velocity of the observer, thus deriving a basic postulate of special relativity and validating the quantum interpretation over our current set of interpretations.

Fig2

FIG. 2. Instantaneous change in phase across waves on x-axis for each value of time t

This interpretation leads to a bunch of derivations I want to explore.  I describe a simple example in the paper for entangled particle decoherence.  Another of my favorites is how the interpretation explains “particle or wave” in the dual slit experiment.  Using this approach, it’s very easy to see that the group wave particle is intact until it nears the barrier with two slits.  At that point the definition of where the particle is becomes very ambiguous–but math will show the particle group wave re-appears after it clears the barrier.  I’ll show some sims once I get them completed with pictures (or tell you that I was unsuccessful.  I’m probably still a crackpot, but I try to be an honest one!)

Agemoz

Tags:, , ,
Posted in Physics | Leave a Comment »

Physics Paper is Done!

May 3, 2019

I have spent the last two years working hard on a journal paper based on some of the work I’ve discussed on this site.  I learned a lot in the process, for example, the importance of substantiating every claim I made, and making sure the more speculative stuff stays out of the paper.  Take a look if you like!  You may need to download and use a PDF viewer–some of the math equations don’t show correctly in the wordpress viewer.

 

Here’s the abstract:

The Dirac equation successfully predicts the evolution of probability amplitudes even for relativistic particle interactions, but it is a causal equation and thus cannot predict non-causal quantum interference effects such as quantum entanglement resolution. An extension of the Dirac equation will require a valid quantum interpretation that derives both quantum interference behavior and the special relativity postulate of constant speed in any frame of reference. None of the current quantum interpretations provide the means to derive the special relativity postulate. Therefore, in this study, I assume a quantum interpretation based on a non-causal form of group wave particles.  The study shows that observation of these group wave particles have a constant speed in all frames of reference and thus the quantum interpretation is a valid basis for both special relativity and the Dirac equation. The result of this study is a first step toward building an extension to the Dirac equation that predicts the non-causal interference effects of quantum mechanics.

edit: replaced wrong (older) version of pdf paper

Agemoz

Tags:, , , ,
Posted in General, Physics | Leave a Comment »

Summary of Findings So Far

February 5, 2018

I took the time to update the sidebar describing a summary of the unitary twist field theory I’ve been working on.  I also paid to have those horrid ads removed from my site–seems like they have multiplied at an obnoxious rate on WordPress lately.

One problem with blogs describing research is the linear sequence of posts makes it really hard to unravel the whole picture of what I am doing, so I created this summary (scroll down the right-hand entries past the “About Me” to the Unitary Twist Field Theory) .  Obviously it leaves out a huge amount, but should give you a big picture view of this thing and my justification for pursuing it in one easy-to-get place.

The latest:  I discovered that the effort to work out the quark interactions in the theory yielded a pretty exact correlation to the observed masses of the electron, up quark and down quark.  In this theory, quarks and the strong force mediated by gluons is modeled by twist loops that have one or more linked twist loops going through the center.  This twist loop link could be called a pole, and while the twist rotation path is orthogonal to the plane of the twist loop, the twist rotation is parallel and thus will affect the crossproduct momentum that defines the loop curvature.  Electrons are a single loop with no poles, and thus cannot link with up or down quarks.  Up quarks are posited to have one pole, and down quarks have two.  A proton, for example, links two one-pole up quarks to a single two-pole down quark.

The twist loop for an up quark has one pole, a twist loop path going through the center of it.  This pole acts with the effect of a central force relation similar (but definitely is not identical to an electromagnetic force) to a charged particle rotating around a fixed charge source–think an atom nucleus with one electron orbiting around it.  The resulting normal acceleration results from effectively half the radius of the electron loop model, and thus has four times the rotation frequency and thus 4 times the mass of an electron.  The down quark, with two poles, doubles the acceleration yet again, thus giving 8 times the mass of an electron.

It will be no surprise to any of you that this correlates to the known rest masses of the electron, up quark, and down quark:  .511MeV, 2.3MeV, and 4.8MeV.

I can hear you screaming to the rafters–enough with the crackpot numerology!  All right, I hear you–but I liked seeing this correlation anyway, no matter what you all think!

Agemoz

Tags:, , , , , , , , , ,
Posted in Physics | Leave a Comment »

First Unitary Twist Field Sim Output–It’s a Three Ring Circus! (Update)

December 24, 2017

UPDATE:  errors in the sim calculations are distorting the expected output–it’s too early to make any conclusions yet.  Corrected results coming soon–the CUDA calculations work in 3D blocks over the image, including overlap borders.  As you might expect, the 4D computation gets complex when accounting for the overlap elements.  I had the blocks overlapping incorrectly, which left holes in the computation that caused the soliton image to be substantially distorted.  I still see strong indications that there will be stable solitons in the results, but need to correct a variety of issues in the sim before drawing any conclusions.  Stay tuned…

The first results from the Unitary Twist Field Theory are in, and they are showing a three ring circus! Here are the sim output pictures. The exciting news is that the field does produce a stable particle configuration that is very independent of the initial boundary conditions and strength of the background state and the neighborhood connection force–the same particle emerges from a wide variety of startup configurations. Convergence appears visible after about 20 iterations, and remains stable and unchanging after 200000 steps. So–no question that this non-linear field produces stable solitons, thus validating my hypothesis that there ought to be some field that can produce the particle zoo. Will this particular field survive investigation into relativistic behavior, quantum mechanics and produce the diversity of particles we see in the real world? I created this theory based on the E=hv constraint that implies a magnitude-free field and a background state, a rotation vector field that includes the +/-I direction, and many other things discussed in previous posts, so I think this field is a really good guess. However, it wouldn’t surprise me at all that I don’t have this right and that changes to the hypothetical field will be necessary.  As usual, as in any new line of research work, it’s quite possible I’m doing something stupid or this is the result of some artifact of how I am doing the simulation–it doesn’t look like it to me, but that’s always something to watch out for.  However, here I am seeing good evidence I have validated this line of inquiry–looking for a non-linear precursor field that produces the particles and force-exchange particles of the Standard Model.

It’s very hard to visualize even with the 4D to 2D projected slices I show here. I color coded the +I (background state) dimension as red, -I direction as black, and combined all three real dimensions to blue-green. Note there is no magnitude in a unitary twist field (mathematicians probably would prefer I call this a R3+I rotation unitary vector field), so intensity here simply indicates the angular proximity to the basis vector (Rx, Ry, Rz, or +/-I). For now, you’ll have to imagine these images all stacked on top of each other, but I’ll see if I can get clever with Mathematica to process the output in a 3D plot.

Studying these pictures shows a composite structure of two parallel R3 rings and an orthogonal interlocking -I ring, and something I can’t quite identify, kind of a bridge in the center between the two rings, from these images. These pictures are the 200000 step outputs.  You can ignore the image circles cursors in some of the screen capture shots, I should have removed those!

More investigation results to come, stay tuned!

Agemoz

Tags:, , , , , , , ,
Posted in Physics | Leave a Comment »

String Theory vs Twist Theory in QFT

November 11, 2016

I’ve worked for some time now on a twist field theory that supposedly would provide a description of how quantized particles emerge, and have been working out the required constraints for the field. For example, it’s very clear that this precursor field cannot be some variation of an EM field like DeBroglie and others have proposed. In order for quantization to occur, I’ve determined that the field cannot have magnitude, it is a unitary R3 + I vector field with a preferred orientation to the I dimension, thus allowing geometrical quantization and special relativity behavior (see previous posts for more details). Particles arise when the twist forms a ring or other closed loop structure. I’ve been attempting to work out enough details to make possible an analytic solution and/or set up some kind of a computer model to see if the quantized particles in the model can somehow represent the particle zoo of reality. As I tried to work out how the field elements would interact with each other, I started to see a convergence of this twist field idea with quantum field theory, the field components would interact in a summation of all possible paths that can be computed using Feynman path integrals. If it were true, I think the twist field theory would add geometrical details to quantum field theory, providing a more detailed foundation for quantum physics.

Quantum field theory assumes the emergence of particles from the vacuum, provided that various conservation properties are observed. All interactions with other particles or with EM (or other) fields take place using specific exchange particles. Quantizing the field in QFT works because only specific particles can operate as exchange bosons or emerge from the background vacuum, but QFT does not provide a means to describe why the particles have the mass that we observe. QFT uses quantized particles to derive why interactions are quantized, but doesn’t answer why those particles are quantized. I worked on this twist field theory because I thought maybe I could go a step further and find out what quantizes the particles of QFT.

At this point, I’ve determined that the fundamental foundation of my theory could be described simply as saying that all of the particles in QFT are twists, some closed loop and some linear. So what? You say potay-to, I say potah-to? Particle, twist, what’s the difference? No, it’s more than that. Particles have no structure that explains why one particle acts differently than another, or why particles only exist with specific intrinsic energies. As I have described in many of my previous posts, describing the QFT component particles as geometrical loops of twists can constrain the possible loop energies and enable only certain particles to emerge. It is a model for QFT particles that I think will provide a path for deepening our understanding of quantum behavior better than just assuming various quantized particles.

I realized that my thinking so far is that the unitary twist field really is starting to look like a string theory. String theory in all its forms has been developed to try to integrate gravity into QFT, but I think that’s a mistake. We don’t know enough to do that–the gravity effect is positively miniscule. It is not a second order or even a tenth order correction to QFT. We have too many questions, intermediate “turtles” to discover, so to speak, before we can combine those two theories. As a result, the math for current string theory is kind of scattergun, with no reasonable predictions anywhere. Is it 10 dimensions, 20, 11, or what? Are strings tubes, or one dimensional? Nobody knows, there’s just no experimental data or analysis that would constrain the existing string theories out there. As a result, I don’t think existing string theory math is going to be too helpful because it is trying to find a absurdly tiny, tiny sub-perturbation on quantum field math. Let’s find out what quantizes particles before going there.

The unitary twist field theory does look a little like strings given the geometry of axial precursor field twists. The question of what quantizes the QFT particles is definitely a first order effect, and that’s why I think the unitary twist field theory is worth pursuing first before trying to bring in gravity. It’s adding quantizing geometry to particles, thus permitting root cause analysis of why we have our particle zoo and the resulting QFT behavior.

I really wish I could find a way to see if there’s any truth to this idea in my lifetime…

Agemoz

Tags:, , , , , ,
Posted in Physics | Leave a Comment »

Quantizing Fields–Twist Field vs. Semiclassical and Canonical Field Quantization

August 28, 2016

I’ve done all this work/discussion here about this unitary twist field scheme and how it uses quantized rotations to a background imaginary axis. While my primary intent is for my benefit (keep track of where I am and to organize my thinking) I’ve tried to make it readable and clear for any readers that happen to be following my efforts. I try to be lucid (and not too crack-potteryish) so others could follow this if they wanted to. To be sure, my work/discussion on the unitary twist field is very speculative, a guess on why we have the particle zoo. However one big thought has been running through my head–if any of you are following this, you would be forgiven for wondering why I’m doing this field quantization work given that there is already plenty of well established work on first and second quantization of fields such as the EM field.

This is going to be a very tough but valid question to elaborate on. Let me start with a synopsis: my work on this precursor field, and quantum mechanics/field theory work are operating on very different subjects with the unfortunate common concept name of quantization. Quantum theory uses quantization to derive the wavelike behavior of particles interacting with other particles and fields. Unitary Twist Field theory uses a different form of quantization to help define an underlying basis field from which stable/semistable particles and fields (such as the EM field) can form.

Let me see if I get the overall picture right, and describe it in a hopefully not too stupidly wrong way.

Both quantum theory and my Unitary Twist Field work reference quantization as a means to derive a discrete subset of solutions concerning fields and particles from an infinite set of possible system solutions. Quantum theory (mechanics, field theory) derive how particles interact, and quantization plays a big part in constraining the set of valid interaction solutions. Unitary Twist Field theory (my work) involves finding a field and its properties that could form the particles and field behavior we see–an underlying field that forms a common basis for the particles and the interactions we see in real life. Quantum theory and the Standard Model currently provide no clear way to derive why particles have the masses and properties that they do, Unitary Twist Theory attempts to do that by defining a precursor basis field that creates solitons for both the stable/semistable particles and force exchange particles required by the Standard Model and quantum theory.

Standard Model particle/field interactions in quantum mechanics (first quantization) is a semiclassical treatment that adds quantization to particles acting in a classical field. Quantization here means extending the classical equations of motion to include particle wavelike behavior such as interference. Second quantization (either canonical or via path integrals, referred to generally as quantum field theory) extends quantization to fields by allowing the fields to spontaneously create and annihilate particles, virtual particles, exchange particles, fields, etc–it’s a system where every force is mediated by particles interacting with other particles. This system of deriving solutions gets generalization extension via gauge invariance constraints, this work gave rise to antiparticles and the Higgs Boson. Quantization here means that particle/field interactions interfere like waves, and thus there is generally a discrete set of solutions with a basis that could be called modes or eigenstates (for example quantized standing waves in electron orbitals about an atom).

The quantization I am using as part of the defining of the Unitary Twist Field is a completely different issue. I’ve done enough study to realize that the EM field cannot be a basis for forming particles, even by clever modification. Many smart minds (DeBroglie, Compton, Bohr, etc) have tried to do that but it cannot be done as far as anyone has been able to determine. I think you have to start with an underlying field from which both particles and the EM field could emerge, and it has to be substantially different than the EM field in a number of ways. I’ve elaborated on this in extensive detail in previous posts, but in a nutshell, quantization here means a orientable, unitary, 3D + I (same as the quantum oscillaor) field that has a preferred lowest energy direction to the positive imaginary axis. This field should produce a constrained set of stable or semistable solitons. If all goes well and this is a good model for reality, these soliton solutions should then match the particle zoo set and exhibit behavior that matches the EM field interactions with particles described in quantum theory and the Standard Model.

I am attempting to keep in mind that a twist field theory also has to be gauge invariant at the particle level, and has to be able to absorb quantum theory and the Standard Model. That’s to be done after I first determine the viability of the unitary twist field in producing a set of particles matching the known particle zoo. This is a truly enormous endeavor for one not terribly smart fellow, so just one step at a time…

Don’t know if that makes things clearer for readers, it does help narrow down and add clarity in my own mind of what I’m trying to do.

Agemoz

Tags:, , , , , , , ,
Posted in Physics | Leave a Comment »

« Older Entries
Newer Entries »