Posts Tagged ‘simulation’

« Older Entries

Comparison of Quantum Field Theory and the Unitary Rotation Vector Field Theory

May 30, 2020

UPDATED with more details on the unitary rotation vector representation of the test interaction (see section UPDATE below)

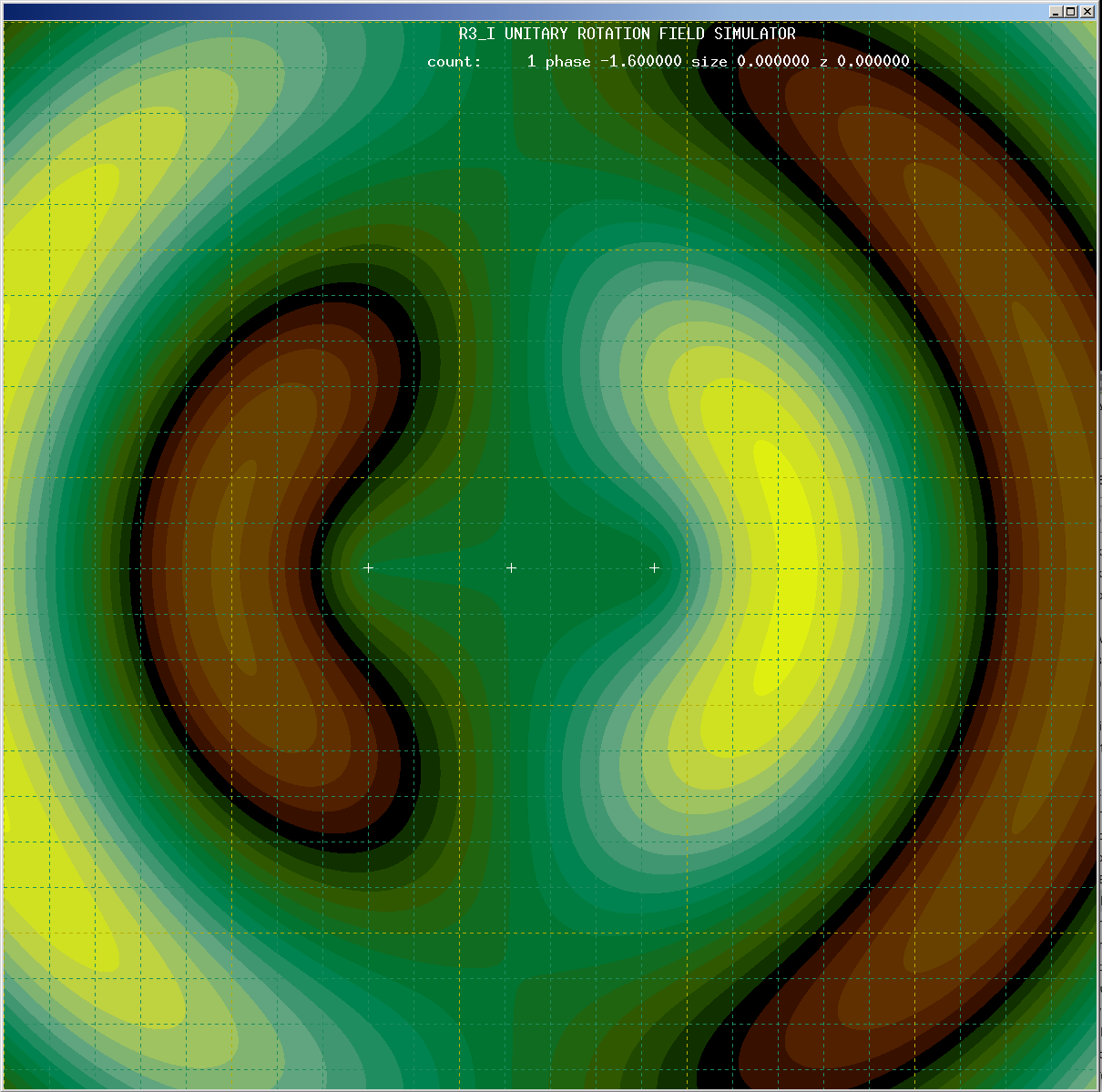
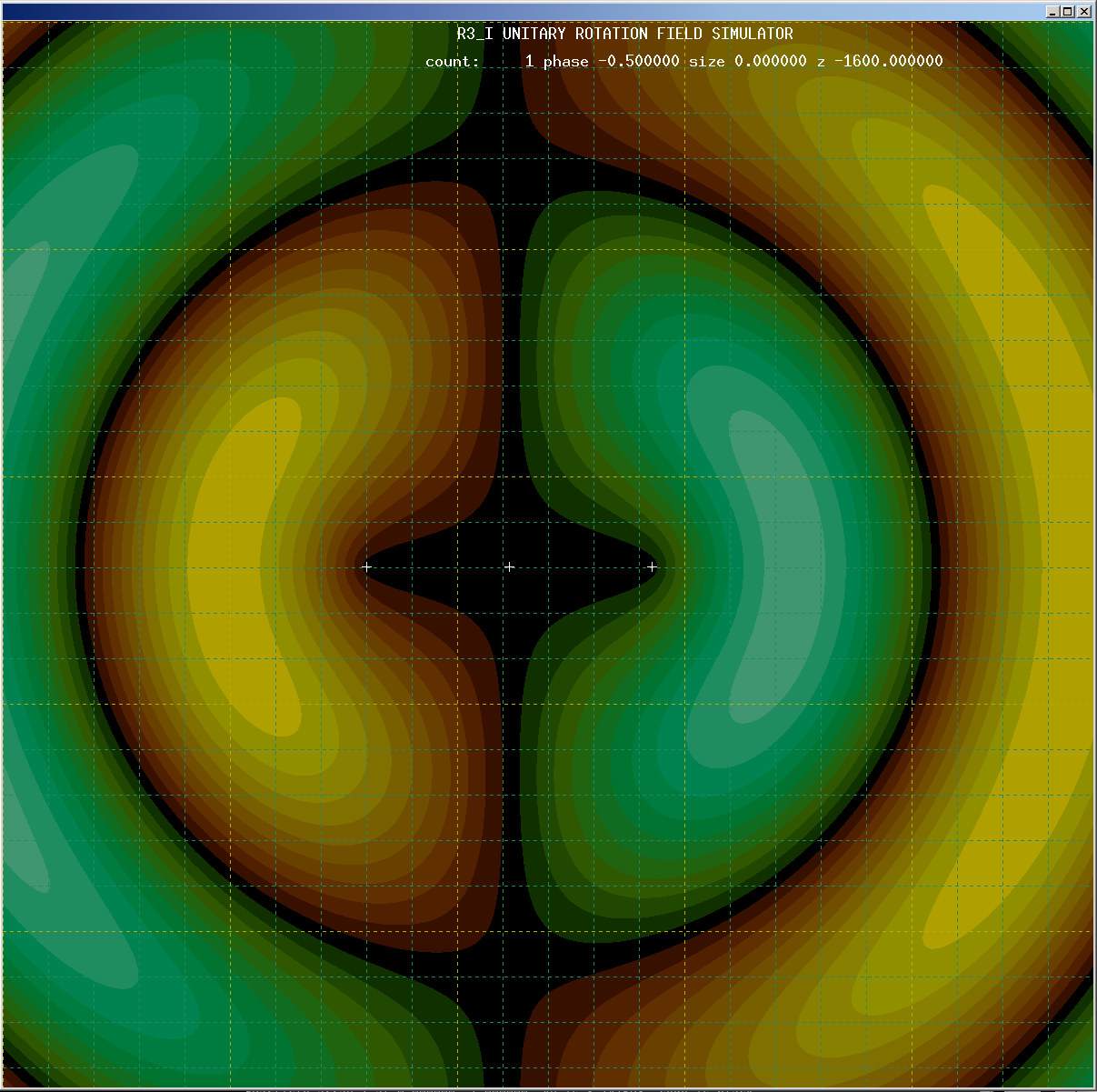
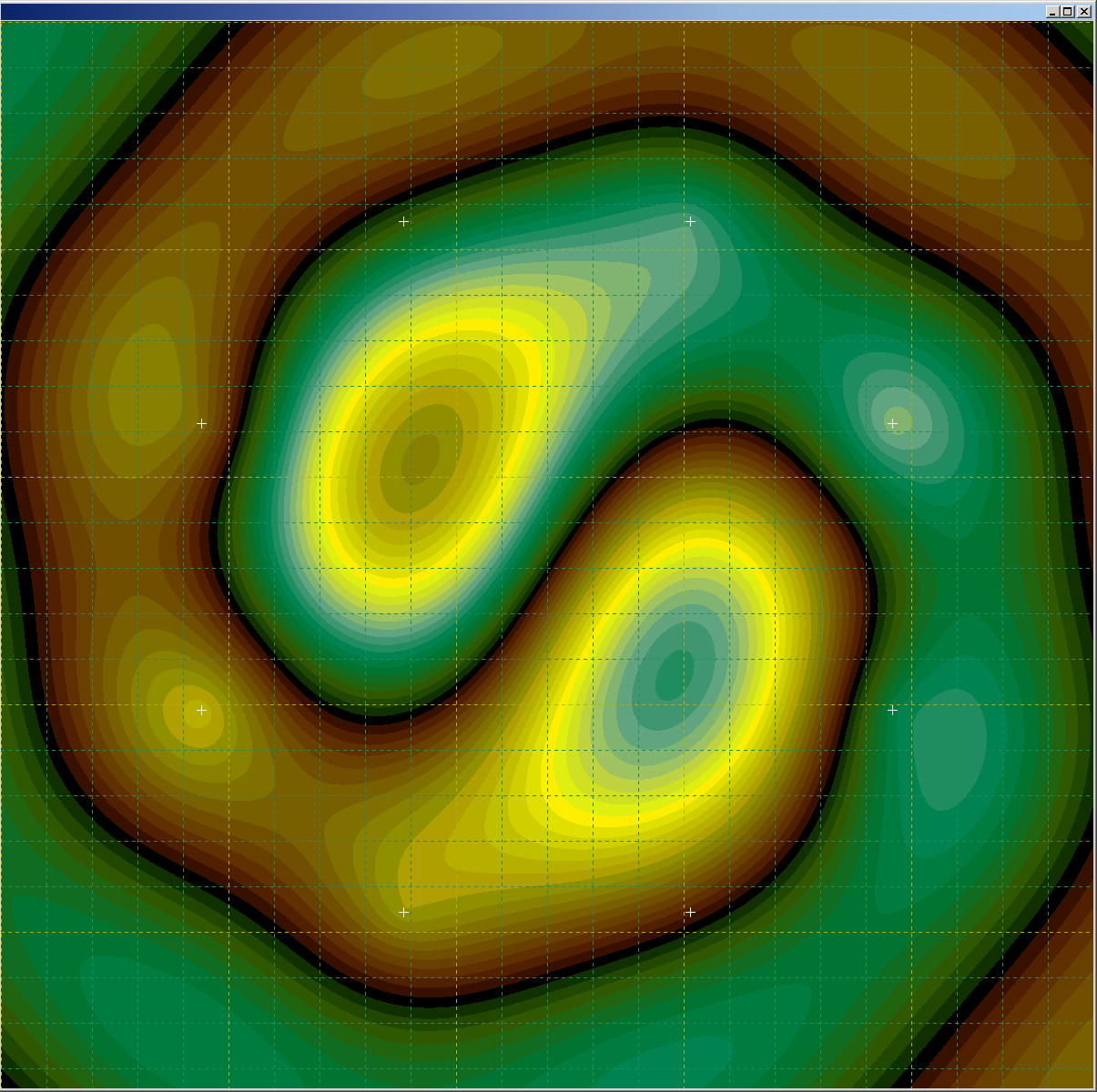
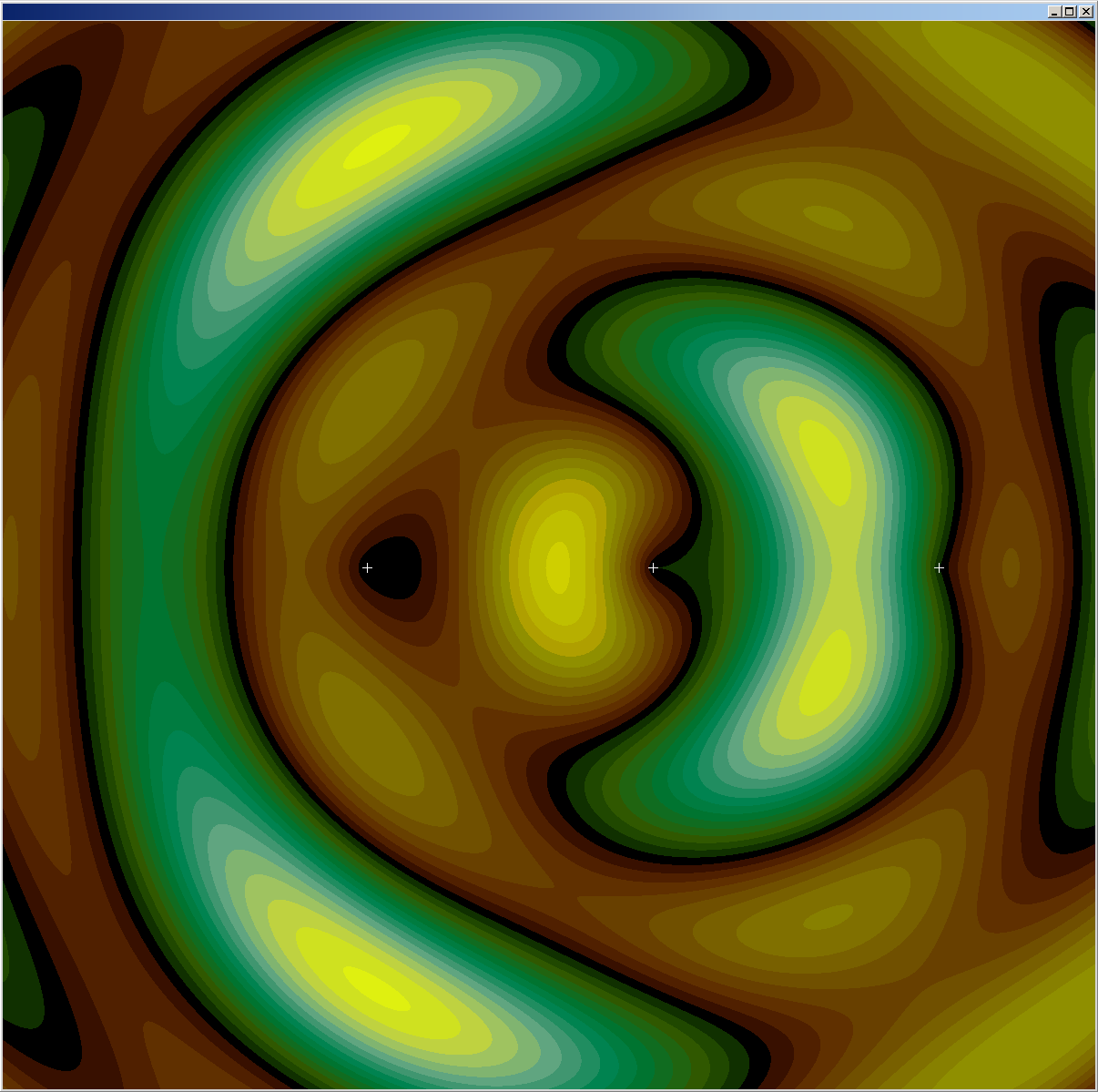
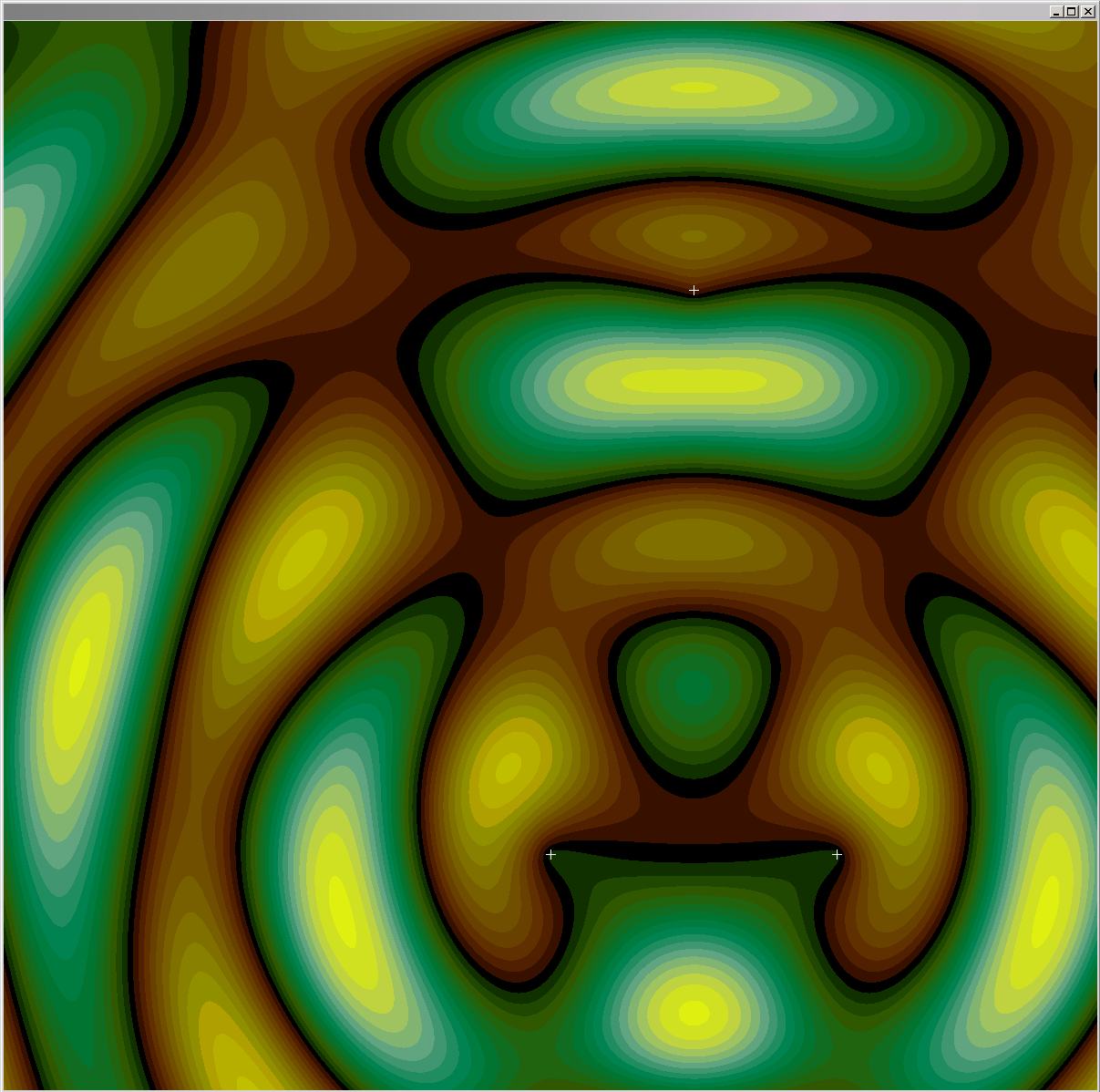
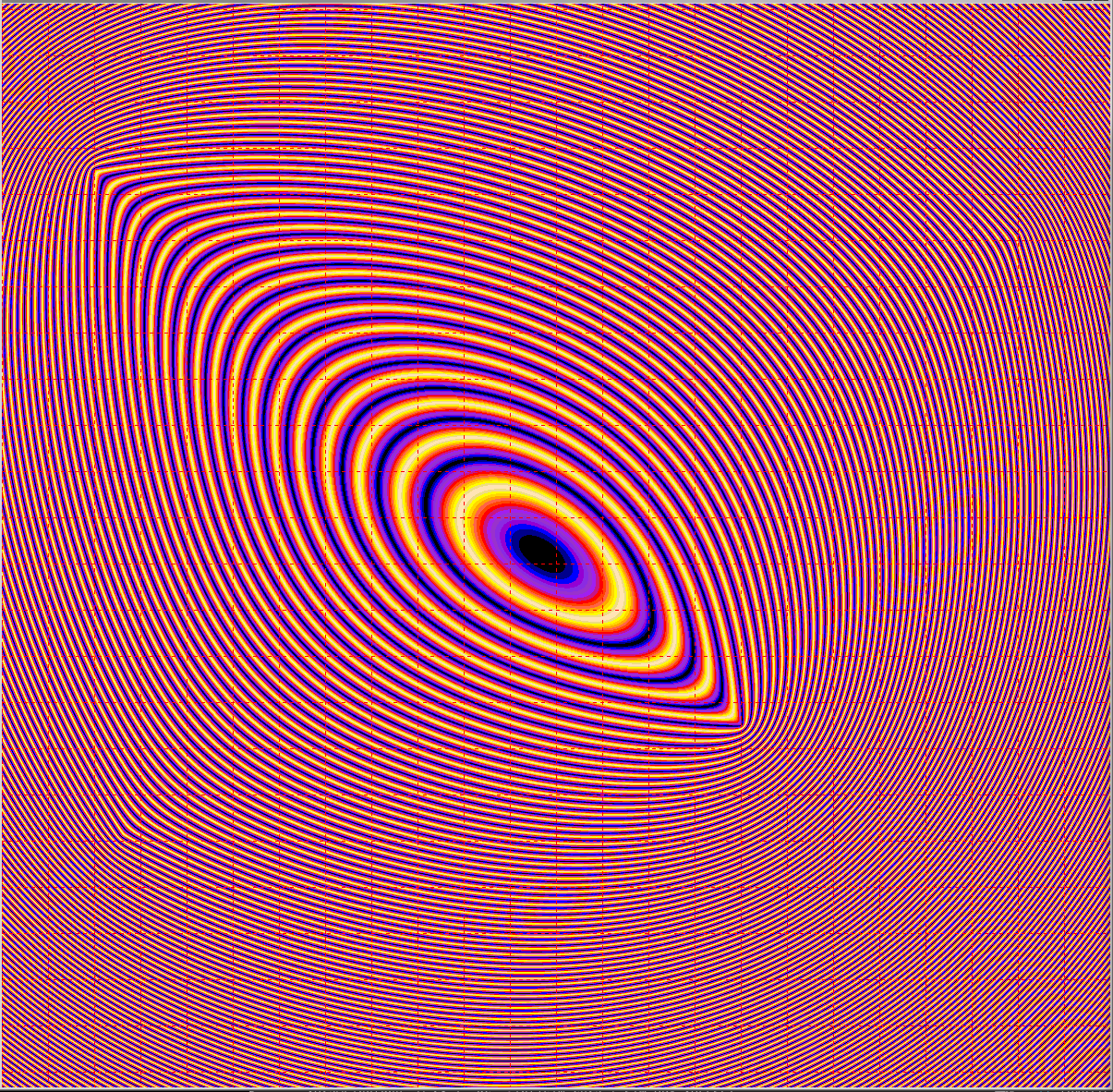
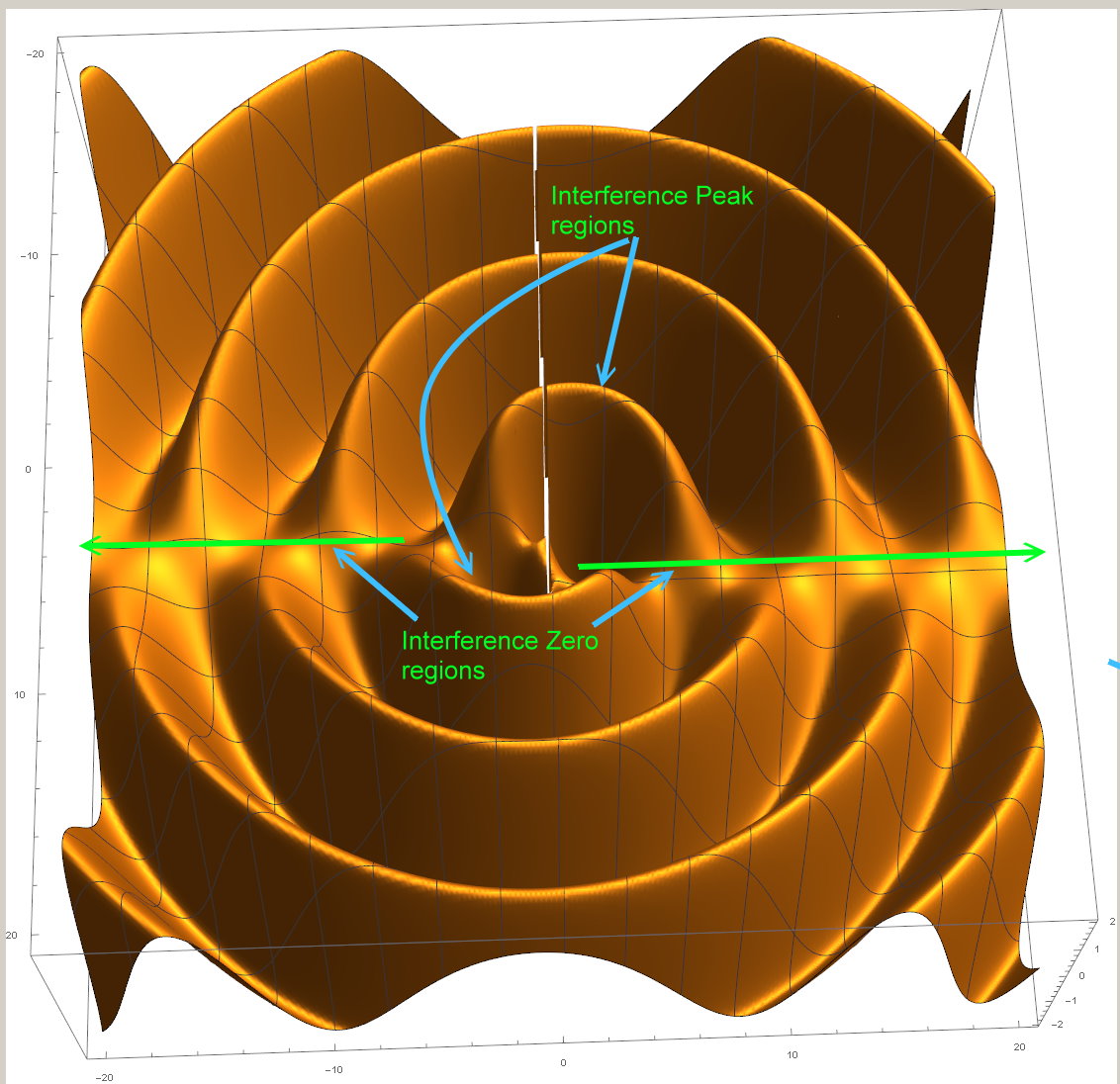
The latest simulations have shown some wonderfully interesting results. The last post showed how the Unitary Rotation Vector Field theory demonstrates particles that can both repel and attract due to quantum interference effects that relocate the stability region of particles. You can read about these results in previous posts, here is a schematic diagram of what happens, along with some sim output pictures demonstrating the principle:

stability_region

I never intended to create a theory that competes with quantum field theory, but the principle of charge attraction and repulsion traditionally is derived directly from quantum field theory methods. So, it seems well worth the effort to compare the two approaches, and what I hope to gain by analyzing the properties of the unitary rotation vector field. While I have run unitary rotation vector field simulations of many particle types and interactions, I think it will be illustrative to compare how each theory handles the simplest interaction of a pair of electrons (charge repulsion).

Quantum field theory solves interactions like these by using LaGrangian mechanics, that is, minimizing the action scalar. Doing a path integral of the LaGrangian over all paths, and setting the the derivative of the action at all points over time to zero yields a motion equation for the particles in the system. This computation will find the path of minimum action and thus will correctly represent reality. More specifically, the interaction of the two electrons is mediated by virtual photons–particles that do not reside on the surface of valid position/momentum solutions in space and time (off mass shell). By prepending a creation operator to the photon wave equation and appending an annihilation operator after it, quantum field theory creates a solution where the time evolution of the electrons go in opposite directions (repulsion).

On the other hand, the unitary rotation vector field (nearly identical to a Pauli spin matrix representation) gets repulsion and attraction in a different way. Both theories do sums of wave paths to find regions of quantum interference, but the wave equation is different. In quantum field theory, the wave equation is the Hamiltonian–the sum of energies such as kinetic energy and the voltage potential in an electromagnetic field. The creation/annihilation operators are probability functions for emergence of virtual particles. The integral is computed over sufficient time so that an operator isn’t left stranded (virtual particles wont conserve momentum in that case).

The unitary rotation vector field is different–it is single valued with only one rotation possible at any given point, and this constrains where particles can exist (the stability region) because the particle phase and the wave phase must match (see the above schematic).

The wave equations in quantum field theory have wave solutions that propagate over time (for example, the propagator in the La Grange equation of action). Solutions depend on virtual particles that don’t obey classical physics. Quantum field theory can’t work without them because on-mass-shell particles will induce the momentum paradox described in the previous post. Nothing propagates in the unitary rotation vector field–each point just rotates, so conservation of momentum works without inducing the paradox.

Probably the biggest reason I pursue the unitary rotation vector field, rather than just sticking with the established science of quantum field theory? The rotation vector field seems to give another possible view of the underlying mechanics of particle interactions that might yield answers not covered by quantum field theory. The most significant possibility comes from how it postulates a formation of elementary particles from quantum interference in a field. There are other reasons, such as the theory doesn’t require renormalization methods, it doesn’t depend on off-mass-shell particles to work, and doesn’t have a probabilistic dependence on when virtual particles form.

Since quantum field computations work, it’s arguable my efforts are a waste of time (and certainly could be wrong, or not even wrong). But my curiosity is here, and so for now I will continue.

Agemoz

UPDATE:  I need to clarify the Unitary Rotation Vector Field representation of the particles involved so you can see exactly how I set up the simulation.  There may be other schemes that work, but this is the approach I used in my simulations.

The unitary rotation vector field is continuous and only rotates a unitary vector (like the Pauli spin matrix).  It can point in any of the three real dimensions in R3 or in one imaginary direction (the background state of the theory).  This is the same vector space as the continuous quantum oscillator field, except that there is no variation in magnitude and you cannot have a zero length rotation vector.

Being single valued, a rotation cannot pass thru from one location to another without affecting each location in the path.  As a result, particles must have the same phase as the sum of wave rotations (that is, quantum interference computed as a path integral) at each particle’s location, this is called the particle’s stability region, shown in black on my simulation images.  A particle cannot exist anywhere except in a stability region, otherwise the location would have to simultaneously have two different rotations. Particles are forced to move when the stability region moves–a well tested example is quantum interference resulting from a single particle passing through two slits.

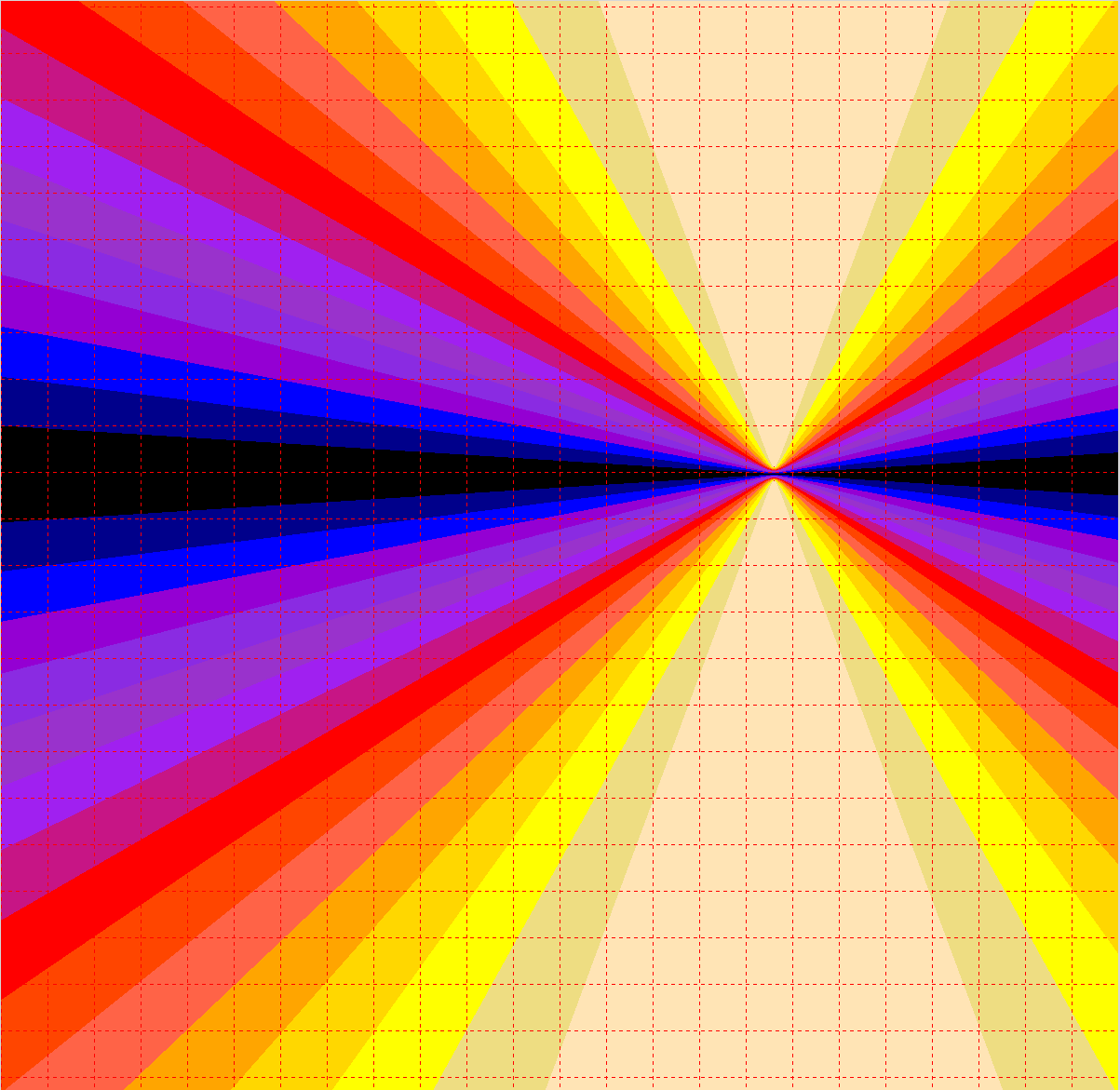
Each field location can be represented by a set of three rotation values–one straightforward basis is a rotation set that resides in the plane that includes the I dimension and the X direction, a rotation that includes both the X and Y directions, and finally one rotation that includes both the X and Z directions.  My simulation uses this basis.  All rotations are modulo 2*Pi (the simulation values go from -Pi to +Pi).

A photon in this theory is modelled with a single quantized vector rotation from the +I direction thru -I and then continues to +I (see the image figure below).  There is a lowest energy state at +I and -I, so once the rotation does one rotation, it stops. The photon also has a translation along some real dimension axis.

photon_carries_momentum

In the interaction of a photon and electron shown in the above simulation pictures, the photon induces either a positive or negative rotation offset to the receiving electron, which causes the electron stability region (via quantum interference) to displace either above or below (attraction or repulsion respectively).  The photon must be able to carry a positive or negative momentum.  You can see that the rotation must lie in the plane that includes both the +I and the translation direction vector (otherwise you will not have photon polarization using any other rotation scheme).  Note that there are two possible rotation directions–either rotation begins moving toward the direction of travel, or away from it, corresponding to the two possible rotation offset directions intercepted by the electron.

The really interesting thing about this configuration is that the photon becomes a momentum carrier, but intrinsically does not have any actual momentum due to its translation.  The source particle emitted momentum is carried by the photon’s rotation but the photon has no momentum of its own (consistent with the fact that photons are massless particles).  This is what allows photons to pass along either negative or positive momentum without inducing the momentum paradox.  That is, shooting a massive particle at a destination particle cannot ever cause attraction, but photons can.

This seems to be a much better scheme for how photons carry electrostatic force than the virtual particle scheme used in quantum field theory.  Virtual particles are just assumed to not obey momentum/position conservation from creation to annihilation, which means I can’t simulate it.  I can only define the interaction as a black box.  It computationally works, (there’s no way ever that I would say quantum field theory is wrong!!!)  but my goal is that the unitary rotation vector approach could lead to a deeper understanding of particle interactions.

Agemoz

Tags:, , , ,
Posted in Physics | Leave a Comment »

Unitary Rotation Vector Field Mimics Electron-Photon Interaction

May 20, 2020

I set up a quantum interference unitary rotation vector field sim with a very basic idealized representation of a two pole “electron” and a much lower frequency one pole “photon” along the z-axis, and here is what I found:

a: The “photon” wave (photon meaning the sim model of a photon in this post) makes the two pole electron unstable at the z = 0 axis position. Instead, the stability region moves along the z-axis depending on the phase of the photon pole. As a result, the quantum interference pattern from all three poles appears to force the electron to translationally move along the axis of the photon z displacement, which matches the expected electron-photon interaction behavior.

b: Depending on the phase of the incoming one-pole photon, I found that the stability region for the two-pole electron can either be below (away from) OR above (toward the photon). Could we at last have an explanation for why electrostatic fields emitted from a source can either repel or attract?

There is a momentum paradox in electrodynamics–if photons have momentum toward an electron, how can momentum be conserved if the electron ends up (due to charge attraction) with momentum in the opposite direction (toward the photon)? Quantum field theory computes that the field itself absorbs the momentum difference (and yes, mathematically that works) but intuitively I rebel at that analysis. The unitary rotation vector field appears to be providing a very elegant solution–quantum interference directs where the electron stability region has to go via wave interference, and in some phase cases it exists toward the photon rather than away from it.

c: It doesn’t matter where you put the photon. I get the same results regardless of the photon offset in the x-y plane (although as mentioned, the z offset causes the electron stability region to move along the z axis).

d: It doesn’t matter what frequency is used for the photon, although the stability region displacement above or below the electron initial position will vary linearly as 1/photon frequency. Higher frequencies cause the photon phase change and hence the change in z displacement to occur at a faster rate, lending credence to the idea that higher momentum photons will induce a larger momentum change in the electron.

e: The only thing the sim seems to get wrong is the absorption of the photon, which should disappear after encountering the two-pole electron. This will require more investigation.

So, in summary, at least on this first pass of testing, the hypothesis that quantum interference in a unitary rotation vector field is responsible for particle formation and particle interactions appears to behave correctly for the electron/photon interaction test.

That by no means is saying that my hypothesized unitary rotation vector field represents reality (if a real physicist were reading about my efforts, he/she probably would wish my efforts would die in a fire if I said something like that) but it looks pretty promising right now. In time and with more work, who knows where this will go–but the real test will be for some qualified researcher to confirm what I am seeing. Until that happens, you should assume that this is unreviewed work (by one author, the kiss-of-death for a research paper) and take it with a bucket of salt…

Agemoz

Here is a picture with the photon in the center, and the z plane is at zero (note this picture cannot be stable, the outside crosses are not in zero delta phase regions)

twopole_z_1_6_phase_unstable

Looking at the same image, the region of stability has relocated closer to the photon (representing electrostatic attraction).

twopole_z_1_6_phase_stable

The region of stability displacement linearly varies as the phase shift induced by the photon, notice the region for a smaller phase shift has not relocated as far from the original electron position:

twopole_z_0_4_phase_stable

Tags:, , , , ,
Posted in Physics | Leave a Comment »

Only Two, Three, or Four Poles Possible in a Quantum Interference Unitary Rotation Vector Field

May 18, 2020

I’ve done extensive work trying to find all possible stable particle configurations using quantum interference, and only three combinations are showing definite stability; solutions exist for two and three poles.  There is one valid set of four poles that statically would be stable but only in three dimensions (tetrahedral shape) but I see problems that indicate such a solution wouldn’t work dynamically (have to really watch out for confirmation bias because so far there is correlation to the real-life particle set) .  It’s geometrically very clear that no 5 pole or higher can exist as a stable solution.

[UPDATE] More results I forgot to mention: A consequence of the 4 pole limit is that a twist ring cannot work. I approximated a twist ring with an 8-pole solution which shows no stability, and geometrically it’s easy to see why (an infinite overlap of wave phase points on every point of the ring). A ring will generate waves from all points about the ring, and there is no possible way this can exist in the single-value unitary rotation vector field. So, the twist ring, long promoted on this site as a valid field solution, bites the dust, at least for the unitary rotation vector field case. This is really interesting because it confirms the experimentally observed infinitely small point concept of current physics, and also seems to validate the Bohm interpretation of an infinitely small core with a non-causal guiding wave for particles. Here’s a picture–note the little crosses are the pole locations with stepwise increments in phase. You can tell that this is unstable because the phase delta between the sum of waves plus the particle phase must be zero and would show here as a black region–but instead many poles do not and cannot reside in a zero phase region. That is indicating that the particle phase and the wave phase are different, an impossibility in this single-valued unitary rotation vector field.

eightpole_unstable

Also, (face-palm moment as I jumped too fast to conclusions) there actually are 5 pole and greater solutions, provided all the poles lie in a line. However, another constraint is emerging where this type of solution may not be stable except in the static case. Working on that one…

Here are pictures for two and three poles:

twopole_updated
threepole_stable_221
threepole_stable_112

I’m now working on a sim where a unitary rotation vector field “photon” approaches and is captured by a field “electron”.  Results shortly–should be interesting and a fairly definitive test for whether the unitary rotation vector field can really model reality.

Agemoz

Tags:, , ,
Posted in Physics | Leave a Comment »

Unitary Rotation Sim Quark Combination Results

May 9, 2020

The latest sims show yet another intriguing connection between three pole simulations and experimentally observed quark combinations.  A couple of posts ago, I wrote a surprising result that only certain three pole configurations were stable.  Those combinations happen to match the valid quark combinations for protons and neutrons, but all other combinations were clearly unstable.  At first I thought, aha, a breakthrough, but after thinking about it I thought quark interactions are extremely complex and such a simple explanation shown by the sim couldn’t be the explanation for valid quark combinations.

Nevertheless, I have continued to explore three pole configurations and came up with another consistency (yes, this is confirmation bias at work here!).  There are two valid three quark configurations, u-u-d (proton) and d-d-u (neutron).  However, only one of them, the proton is stable–a free neutron will decay into a proton, an electron, and a neutrino after a while unless accompanied by a proton in an atomic nucleus.

Curiously, the three pole simulations are showing a similar disparity.  The geometry of the two long wavelengths plus one 1/2x short wavelength is easy to see, you can set it up as an isosceles  triangle.  Here is the sim stability test for that case:

threepole_224_stability

But the opposite case using one long wavelength and two 1/2 short wavelengths cannot produce a valid configuration, there is no way to lay this out such that wave phases match (try to lay out a triangle with two short sticks and one 2X longer stick, you can’t–they form a line).  I have tried a number of sim configurations to get a valid configuration, and haven’t found one yet–just thinking about the geometry seems to show there cannot be one.  Trying to line up the poles in any spaced combination gives unstable results:

threepole_442_stability

What if we set up a known stable quark configuration (a neutron and a proton, three up quarks and three down quarks?)  This requires 6 poles, but I haven’t found any configuration that works, at least in the 2D plane.  You have to set up the poles so all 6 locations have identical phase matches for three up wavelengths and three down wavelengths (due to the unitary rotation field requirement, every location must be single valued, that is, have identical wave phase rotation values from every pole).  Locating the poles so the long wave poles (up particles) are points on an equilateral triangle, and placing the short wave poles (down particles) on a nested upside-down triangle looked promising but doesn’t work.  There are pairs going from the up poles to the opposite down poles that have a phase change of sqrt(3)/2, and phases won’t match.  If there is a solution, maybe in 3D, I haven’t figured it out yet.  And, it’s quite likely that stability in this configuration (an ionized iosotope of hydrogen with one neutron, technically ionized deuterium) conferred due to a particle property not modeled in the sim.

Or I’m certainly open to the possibility that the sim doesn’t model reality at all.  It is intriguing, though, how many real-life quark properties are showing up in the sim.  I’ll continue to investigate.

Agemoz

Tags:, , , ,
Posted in Physics | Leave a Comment »

Unitary Rotation Vector Field Three Pole Solutions Exactly Mimic Quark Combinations

April 25, 2020

I apologize for overposting here–I’m definitely going to be overdoing it–but I just felt like I had one more result to post (UPDATE below).

Most three pole solutions just produce the infinite wave results that are not sustainable as a real representation of particles, I just see the infinite series of wave rings.  But I thought, what if I tried to duplicate the three quark up/down configurations?  I place three poles in a triangle, and gave them all the same energy.  Nope, infinite rings.  Next, gave one of the poles half the frequency like an up quark.  Nope, still infinite rings.  Now, give it an antipole rotation: voila!  a stable particle configuration:

three_pole_m2_4_m2

In fact, I tried all combinations of “up” particles and “down” particles, and guess what–only two produced particles, the anti-up, down, down and the up, anti-down,anti-down configuration!  Yow–that was exciting.

However, Feynman’s ghost is here, and he says: be skeptical.  This may just have a stupidly simple reason, not a physics breakthrough.  It could just simply be the fact that 1 + 1 – 2 = 0, and -1 -1 + 2 = 0.

{update}:  quark sets have extremely complicated interactions and I now doubt that this configuration directly represents them (for example, where is the mass of the gluons).  It might give a clue of internal details of a quark set, but there has to be more to it.

Something much more significant is showing up with these sim results–the hypothesis that a testable principle exists.  It is this:

Quantum interference is responsible for redirecting particles along wave interference peaks–and also for creating those particles.

It doesn’t matter that we are talking wave functions (probability distributions) rather than actual waves, the redirection still happens.

It’s becoming very clear from these sim results that at certain wave frequencies, the effect of quantum interference must control the motion of poles because in the unitary rotation vector field, every field location is single valued (only one possible rotation at each point).  As a result, the quantum interference redirection that occurs in the two-slit experiment can also cause poles to encircle each other in a stable pattern.  I’m about to set up an experiment to directly test this principle.

More pictures to come…

Agemoz

Tags:, , , , ,
Posted in Physics | Leave a Comment »

Unitary Rotation Field Simulator: More Results

April 25, 2020

I’ll try not to post here too often, but a whole ton of results are coming back from different experiment configurations using the Unitary Rotation Vector Field simulator.  One thing that became immediately obvious is that stable solutions are not going to come from most pole configurations–the spreading waves you saw on the previous post aren’t sustainable in a universe full of particles.  I was pretty suspicious of something not right when I could make the dipole disappear entirely (see previous post).

I discovered a whole new ball game when I set up opposite pole dipoles:

dipole_1

The wave pattern disappears as the poles cancel out.  The residual rotations shown occur because I have yet to apply the effect of the I dimension (the background state referred to in previous posts about the theory I’ve been working on).  Here is a picture of two such dipoles of different frequencies:

two_dipoles_1

There are wide space dipoles representing lower energy solutions:

dual_2pi_dipole

Note that I’m just barely scratching the surface of the properties of this amazing field.  I’m only using one of the rotation modes (there are three in the R3+I field of the theory), I don’t have the background state turned on yet, I am currently only studying 2D configurations, and I have not turned on any time dependent characteristics, in particular, how such particles will move.  There’s so much to do and to document!

Agemoz

Tags:, , , , ,
Posted in Physics | Leave a Comment »

Unitary Rotation Field Sim First Light

April 24, 2020

The unitary rotation vector field is a promising candidate for an underlying field that theoretically should produce solitons, quantum effects, and special relativity.  In order to see if the field really could work or is just snake oil, I wrote a simulator.  That has taken a while to get working, but now I’m starting to get results that have been truly fascinating.

I’ve posted a ton of stuff about this field in previous posts.  I’ll go over a summary:  E=hv is true for all particles, and has led to a realization that a precursor field underlying our existence would have to have one degree of freedom per field element.  In contrast, an electromagnetic field has at least two: vector direction and vector magnitude.  This precursor field must have vector direction, so I posited that existence must be based on a unitary magnitude rotation vector field.  Years of thinking have led to all kinds of insights, including that such a field has to obey special relativity–a conclusion significant enough that I wrote a paper on it.  As I worked with this field, I came to the conclusion that such a field would support formation of solitons.  I also discovered that such a field would produce quantum effects such as the two-slit experiment interference pattern.

I have found a vast gold-mine of interesting consequences resulting from such a field to the extent that I felt a deeper dive into writing a simulator was worth the trouble.  After a long period of time, I now have initial results, and the very first pictures that were output made me realize what a very unique animal the unitary rotation vector field is.  Usually when we see interference effects between two oscillating sources (or the wave interference pattern that emerges from a two slit experiment barrier, we see something like this:

interference_pattern

But when I set up two sources using the unitary rotation vector field, I was so surprised that I thought there was something wrong with the simulator.  But then I thought about it for a while and realized–a unitary rotation field is a very different critter than what we are used to when we study EM theory or quantum mechanics.

Here is a picture of two identical (same wavelength) particles separated by a substantial distance.  It should be really clear that between these two particles the interference of rotation waves disappears.  The two particles are effectively entangled, and in this vector field the waves interfere along the path between them.

two_particle_1

Removing one of the two particles instantly removes the interference and the stable path between them.

one_particle_1

Now this is where things get bizarre beyond belief:  add a *third* particle nearby in space, and the wave pattern of the first two completely *disappear*!!  Going to four or more particles, the wave pattern causes a single new entity to appear in the center.  This aint your Gramma’s EM field here!

three_particle_unrelated_1

four_particle_same_1

five_particle_1

I will stop here, but I haven’t even begun–this is a 5D sim, I’m just testing 2D configurations to test it.  I am just capturing a single slice, but 3D configurations will be fascinating to uncover.  And–we are talking static configurations–wait until you see how these things move!

You may be completely skeptical that any of this connects with reality, or passes that ultimate test of new physics, that it predicts something new.  However, I am fascinated by the potential of this new tool, the unitary rotation vector field simulator, to lead to new insights about the theory I’ve worked on for so long.

Agemoz

Tags:, , , ,
Posted in Physics | Leave a Comment »

Quantum Interference Defines a Soliton: Part II, Computed Images

June 20, 2019

Here are actual computed results of how the interference pattern moves for a dual interference source.  In my previous post, I described how a moving interference pattern will alter the location displacement of the interference sources, which leads to the conclusion that quantum interference should enable stable solitons.  There, I showed a schematic representation of what should happen.  Here is visual computed proof that what I described actually happens:  The first picture shows no orthogonal displacement of the interference sources, so the interference paths are symmetric about the interference source X axis.  However, the following pictures demonstrate more and more successive orthogonal Y displacement, causing the interference peak paths to rotate in such a way as to displace the nearby interference source.  This assumes that the interference source will follow the rotating interference path–we know this is true due to experimental verification via the two-slit experiment as one example.  As a result, you should see that moving one interference source should cause the adjacent interference source to move in the opposite direction, causing the two sources to orbit like a binary star (see the previous post for details).

Notice the white line, this is the X axis reference direction to help assess the interference path rotation as y-axis displacement is added to one of the interference sources.  These examples show just one possible interference system–it shouldn’t be unreasonable that I conclude that all planar non-degenerate interference cases should behave the same way.  Things get really interesting when one of the sources is rotated into the Z axis, and when a third source is placed on the Z axis, and when the wavelength of one of the sources is doubled or multiplied by other factors such as 1/3 or 2/3.  More to come…

Agemoz

Edit:  My initial analysis (see previous post) showed that the two interfering sources would cause a rotating interference pattern if one were to move past the other in the direction orthogonal to the axis that both sources lie on.  I could show that there would be an induced motion to the second source if the first source were moved orthogonally, but did not know what would keep the second source from moving centripetally (moving away from the center).  Closer examination (see zoomed in picture) shows that there is a potential well in both the X and Y direction–the interference pattern itself is what constrains the radius of the orbiting path.  I do not need to invoke something like the speed of light to keep the orbital path confined to its radius.

sum_radials_00

sum_radials_10

sum_radials_20

 

sum_radials_30

Edit:  My initial analysis (see previous post) showed that the two interfering sources would cause a rotating interference pattern of rays if one were to move past the other in the direction orthogonal to the axis that both sources lie on.  I could show that there would be an induced motion to the second source if the first source were moved orthogonally, but did not know what would keep the second source from moving centripetally (moving away from the center).  I tried to bring in something, the speed of light, to confine the radius of the interference particle orbit, but soon felt like this was a flaw in my scheme for describing a soliton via interference (this is the same reason that various DeBroglie/Compton schemes using an EM field fail).  However, closer examination (see zoomed in picture) shows that the interference pattern is a potential well in both the X and Y direction–the interference pattern itself is what constrains the radius of the orbiting path.  The rays in the previous images are actually interference zeroes, not peaks–the particles will follow a path defined by the peaks.  I do not need to invoke a contrivance like the speed of light to keep the orbital path confined to its radius.

interference_well

Agemoz

Tags:, , ,
Posted in Physics | Leave a Comment »

Details of the Linear Twist Sim

January 9, 2018

(Updates 1 and 2 below)

It’s been an amazing week working on the unitary twist field sim.  Most of the kinks in the sim coding are fixed, and what I’m finding in the sim results I think are astonishing.  Here’s what I’m finding:

a. There is now little doubt in my mind that there is a class of precursor fields based on a rotation (unitary) vector field that produces stable linearly propagating twist particles.  I’ve attempted a geometric proof, and within the limits of the assumptions I am making, the particles appear to have to be able to exist in this type of field and are stable, and so far the sim results are confirming this.

b.  An unexpected result from the sim–the particles have to move as a single rotation at the limiting speed of the sim.  This is exciting because photons cannot exist unless they move at the speed of light, and this sim shows linear twists match this behavior.  As I concluded in my last post, I realized that special relativity has to have a part to play here and in the sim it shows up as only one possible speed for the linear twist.

c.  You cannot form a stable linear twist unless you do one full rotation as defined by the local background state.  Any other partial twist dissipates (or has to be absorbed by something, e.g, virtual particles).  There is an asymmetry in the leading and trailing edge angular momentum of any linear twist–the only way to resolve this is if both ends have the same change of momentum (leading edge incurs a momentum in the next cell, the trailing edge cancels out that momentum).  This property prohibits a twist from being stable unless it completes a rotation, in which case the same change in momentum happens on both the leading and trailing edge.

d.  It is looking probable (but not proven yet) that you can curve the twist path depending on the change of rotation vectors in the path of the linear twist.  As mentioned in one my prior posts, a closed loop will create a changing tilt of rotation vectors internal and external to the loop, thus (in theory) sustaining the closed loop.  This is a big difference between this precursor field and attempts to create stable particles out of an EM field.  You cannot change the path of a photon with some EM field.  However, for the unitary twist field, I’ve already shown that this should be possible geometrically (see back a few posts), but now I need to confirm it with a sim.

UPDATE 1:  here is a picture–probably the most unimpressive picture ever produced by a GPU graphics card!  Nevertheless, there’s a lot of computing that was done to generate it, and clearly shows both propagation and preservation of the emitted twist.  The junk to the upper left is left over from the initial conditions that emitted the twist, I’ll fix the startup code shortly, but I thought you’d like to see the early results that I thought were exciting…

UPDATE 2:  Better pictures coming.  Just like with real photons, I can make these particles any length, modeling the continuous range of frequencies available.  What is shown above is a fairly short “photon”, but I now have pictures of much lower frequency, hence longer, photon wave rotations.  I am still getting perfect reproduction of the photon model as it travels, thus solidifying the conclusion that this field yields stable solitons.  Next up–geometrically I can see that I should be able to get two parallel photons to lase–that is, phase lock.  I’ll start the sim with two out-of-phase photons near each other and see if they lock.  Stay tuned!

end of UPDATE 1 and 2

My biggest concern with thinking I have found something interesting as opposed to “not even wrong” or trivial is that I would have expected at least a few thousand real physicists would have already found this field behavior, perhaps fleshed this out a lot more than I have, and found it wanting as a theory underlying the formation of real-world particles.  This thing is simple enough that I just cannot believe that a lot of people haven’t already been here. I also still have a ton of unanswered questions (for example, issues with the background state concept, whether the +/-I state is necessary, and so on).

So–other than having a lot of fun exploring this, I don’t see anything yet that means I should write a paper or something.  I’ll keep plowing away.  As an uncredentialed amateur, I know it’s more likely I’ll win the lottery than being taken seriously by a professional researcher, and I’m fine with that.

One thing that’s going to be really fun is setting up a sim of a major collision of some sort–I hope I don’t induce a cybernetic singularity and wipe out the universe…. 🙂

Agemoz

Tags:, , , , , , , ,
Posted in Physics | Leave a Comment »

Sim Works for Linear Twists

January 1, 2018

Happy New Year with hope for peace and prosperity for all!

I now have the sim working for one class of particles, the linear twist.  I fixed various problems in the code and now am getting reasonable pictures for both the ring and the linear twist.  Something is still not right on the ring, but the linear twist is definitely stable with one class of test parameters.  This is an important finding because my previous work seemed to be unable to create a model of a photon (linear twist), so I had focused on the ring case.  However, last night (New Year’s Eve, what a great way to start the New Year!) I realized the problem was my assumptions on how to set up the linear twist initial conditions.

Discrete photons are always depicted as a spiral rotation of orthogonal field vectors in a quantized lump.  I could not make my sim do this, both ends of the lump would not dissipate correctly no matter how I set up the initial conditions and test parameters–the clump always eventually disappeared.  I suddenly realized this picture of a photon is not correct–you have to go to the frame of reference of the photon motion to see what’s really going on.  The correct picture in the photon’s frame of reference is not a clump nor a spiral, but simply a column of vectors all in phase from start to finish (emission and absorption).  It’s the moving frame of reference at light speed that makes the photon ends appear to start and stop in transit.  The sim easily simulates the column case indefinitely.  It also should correctly simulate the ring case for the same reason–and in this case since the frame of reference goes around the ring, the spiral nature of the twist becomes apparent in the sim.  It should also create an effective momentum (wants to move in a straight line) to counteract the natural tendency to shrink into non-existence, but I don’t have the correct test parameters that that is happening yet.

One thing that should please some of you–all of you?  🙂   The background state so far is not necessary to produce these results!  That concept was necessary to produce a quantized lump for the linear photon, but as I noted, that’s not how photons work in their frame of reference.  That simplifies the theory–and the sim computation.  And, most importantly as I suggested in the previous post, seems to validate the concept of assuming that a precursor rotation (twist) vector field can form particles.

Agemoz

Tags:, , , , , , , , , ,
Posted in Physics | Leave a Comment »

« Older Entries